Abstract
We determine the efficiency of a delivery system in which an unmanned aerial vehicle (UAV), or a fleet of UAVs, provides service to customers while making return trips to a truck that is itself moving. In other words, a UAV picks up a package from the truck (which continues on its route), and after delivering the package, the UAV returns to the truck to pick up the next package. Although the hardware for such systems already exists, it is not yet understood to what extent such an approach can actually provide a significantly improved quality of service. By combining a theoretical analysis in the Euclidean plane with real-time numerical simulations on a road network, we conclude that the improvement in efficiency due to introducing a UAV is proportional to the square root of the ratio of the speeds of the truck and the UAV.
Summary
이 논문은 드론과 같은 무인항공기와 트럭을 함께 사용하는 배달 시스템의 효율성을 판단한다. 유클리드 평면의 이론적 분석과 도로망에서의 실시간 시뮬레이션을 결합하여 무인항공기 도입에 따른 효율 향상은 트럭과 무인항공기의 속도 비율의 제곱근에 비례한다는 것이 결론이다.
본문 내용
최근 교통과 물류에서 가장 많이 언급되는 것 중 하나가 드론의 잠재적인 사용에 관한 것이다. 특히 배송 시스템에 드론을 많이 활용하고자 하는데 아마존의 Amazon Prime Air, 구글의 Project Wing, DHL의 Parcelcopter 등을 예시로 들 수 있다.

Amazon Prime Air

Project Wing

Parcelcopter
여기서 last-mile delivery의 수요가 증가할 것이라는 언급이 있다. 라스트 마일이란 상품이 최종 목적지까지 배송되기 위한 과정으로 상품을 개인 소비자에게 직접 전달하기 위한 배송 마지막 구간을 의미한다. 즉, 무인정찰기를 배송시스템에 도입하여 하늘과 도로를 통해 배송함으로써 차세대 물류 시스템을 수행할 것이라는 전망이다. 무인항공기 기반 배송 시스템은 장단점이 명백하게 있는데 일단 드론은 운송 비용이 낮고 사람의 개입없이 운행할 수 있으며 도로 교통에 영향을 받지 않기 때문에 빠르게 운행할 수 있다. 그러나 운반 용량이 매우 작고 이동 반경이 짧으며 충전을 자주 해야한다.
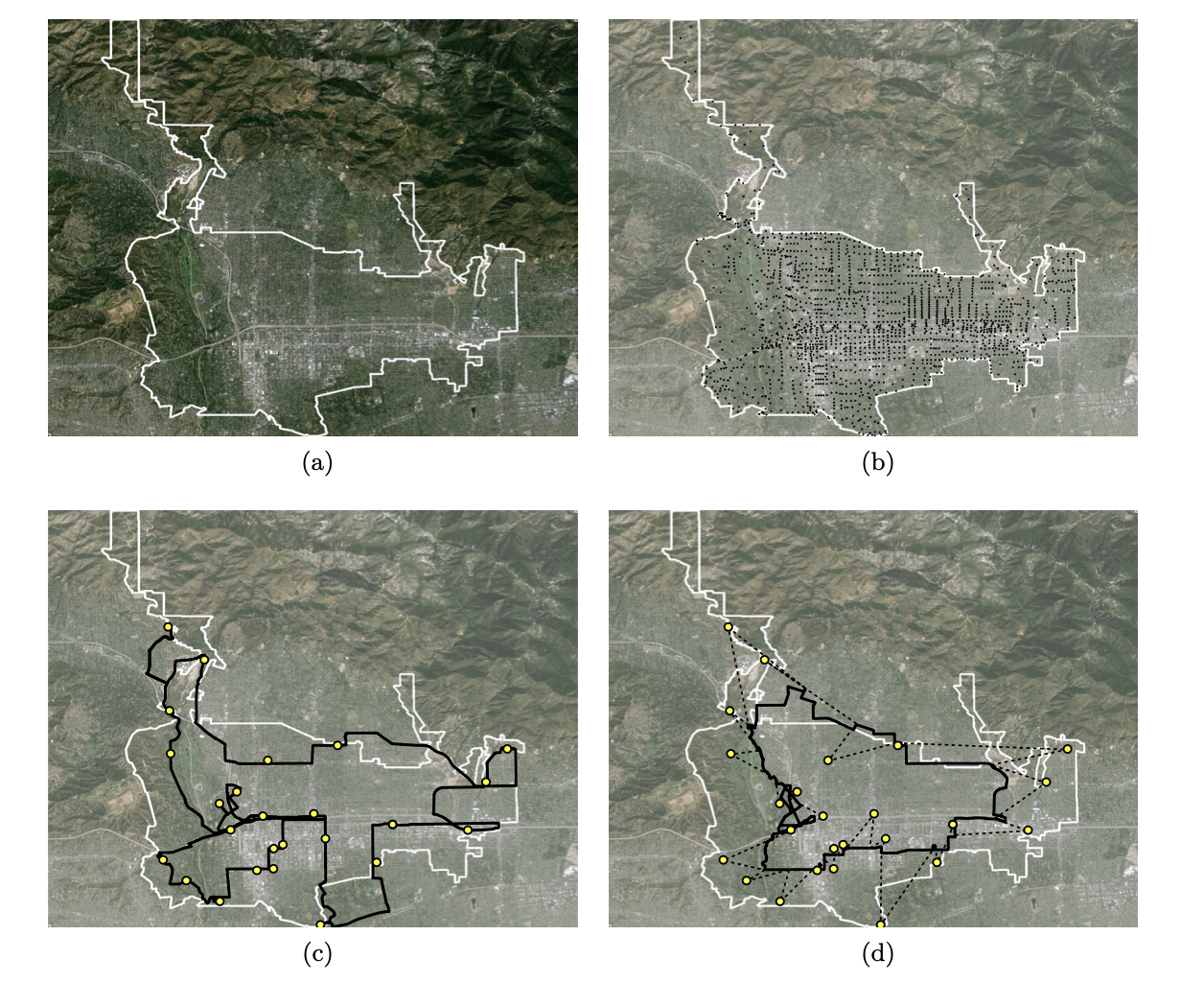
이 논문의 목적은 드론과 트럭을 함께 사용하여 배송하는 것의 효율성을 판단하는 것이다. 이러한 실제 시스템 중 하나가 HorseFly이다. 실제로 어느 정도까지 서비스 품질을 향상시킬 수 있는지 파악되지 않았기 때문에 수학적으로 얼마나 개선을 실현시킬 수 있는지 언급한다.
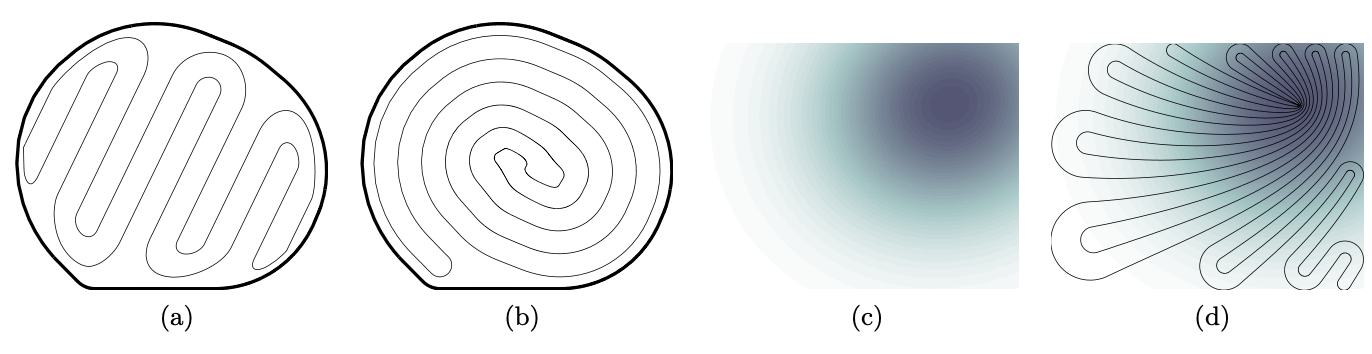
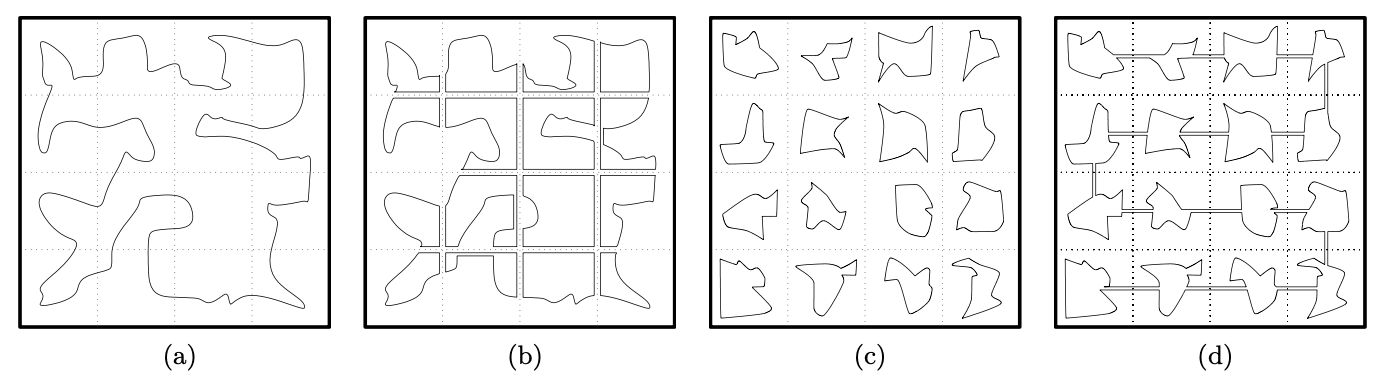
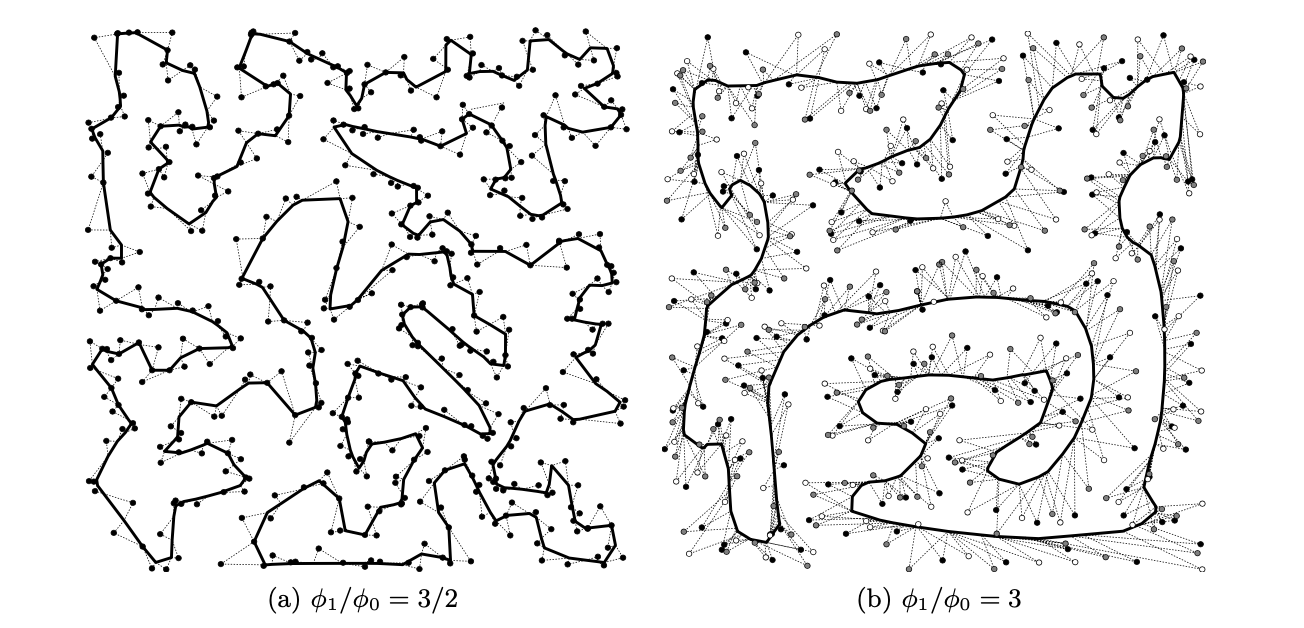
$n$개의 고객이 있다고 가정하며 트럭의 속도는 $\phi_0$, 드론의 속도는 $\phi_1$로 나타낸다. ($\phi_0<\phi_1$) compact planar region을 $\mathcal{R}$, $\mathcal{R}$에서의 loop를 $\mathcal{L}$, 모든 loop $\mathcal{L}$의 집합을 Loop($\mathcal{R}$)이라 하면 $d(x, \mathcal{L})$를 다음과 같이 $x$와 loop $\mathcal{L}$ 사이의 거리로 나타낼 수 있다. $$ d(x, \mathcal{L})=\min _{x^{\prime} \in \mathcal{L}}\left\|x-x^{\prime}\right\| $$ 이는 일반적인 유클리드 거리를 나타내고 {1,...$n$}의 순열 집합을 $S_n (\sigma \in S_n)$이라 하면 항공기에서 집합 $S$의 $\epsilon$-neighborhood는 다음과 같이 $N_{\epsilon}(\mathcal{S})$로 쓰인다. $$ N_{\epsilon}(\mathcal{S})=\left\{x \in \mathbb{R}^{2}: \min _{x^{\prime} \in \mathcal{S}}\left\|x-x^{\prime}\right\| \leq \epsilon\right\} $$ 먼저 앞서 언급한 horsefly routing problem을 공식적으로 정의한다. 트럭 1대와 드론 1대에 대해 $p_1,...,p_n$을 포인트의 집합이라 한다면 다음을 만족하는 최적 솔루션이 $p_1,...,p_n$의 최적 horsefly tour이다.
논문 결과는 다음과 같이 정리할 수 있다.
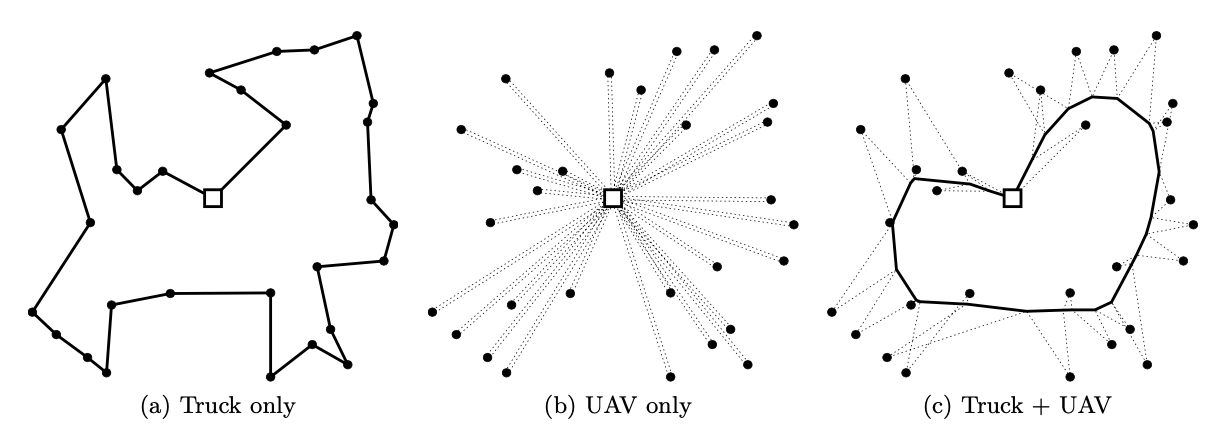
이 논문의 목적은 드론과 트럭을 함께 사용하여 배송하는 것의 효율성을 판단하는 것이다. 이러한 실제 시스템 중 하나가 HorseFly이다. 실제로 어느 정도까지 서비스 품질을 향상시킬 수 있는지 파악되지 않았기 때문에 수학적으로 얼마나 개선을 실현시킬 수 있는지 언급한다.

$n$개의 고객이 있다고 가정하며 트럭의 속도는 $\phi_0$, 드론의 속도는 $\phi_1$로 나타낸다. ($\phi_0<\phi_1$) compact planar region을 $\mathcal{R}$, $\mathcal{R}$에서의 loop를 $\mathcal{L}$, 모든 loop $\mathcal{L}$의 집합을 Loop($\mathcal{R}$)이라 하면 $d(x, \mathcal{L})$를 다음과 같이 $x$와 loop $\mathcal{L}$ 사이의 거리로 나타낼 수 있다. $$ d(x, \mathcal{L})=\min _{x^{\prime} \in \mathcal{L}}\left\|x-x^{\prime}\right\| $$ 이는 일반적인 유클리드 거리를 나타내고 {1,...$n$}의 순열 집합을 $S_n (\sigma \in S_n)$이라 하면 항공기에서 집합 $S$의 $\epsilon$-neighborhood는 다음과 같이 $N_{\epsilon}(\mathcal{S})$로 쓰인다. $$ N_{\epsilon}(\mathcal{S})=\left\{x \in \mathbb{R}^{2}: \min _{x^{\prime} \in \mathcal{S}}\left\|x-x^{\prime}\right\| \leq \epsilon\right\} $$ 먼저 앞서 언급한 horsefly routing problem을 공식적으로 정의한다. 트럭 1대와 드론 1대에 대해 $p_1,...,p_n$을 포인트의 집합이라 한다면 다음을 만족하는 최적 솔루션이 $p_1,...,p_n$의 최적 horsefly tour이다.
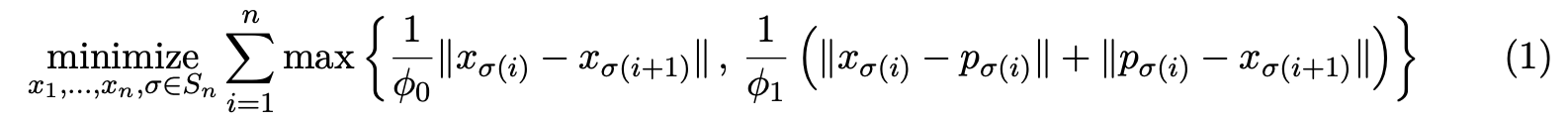
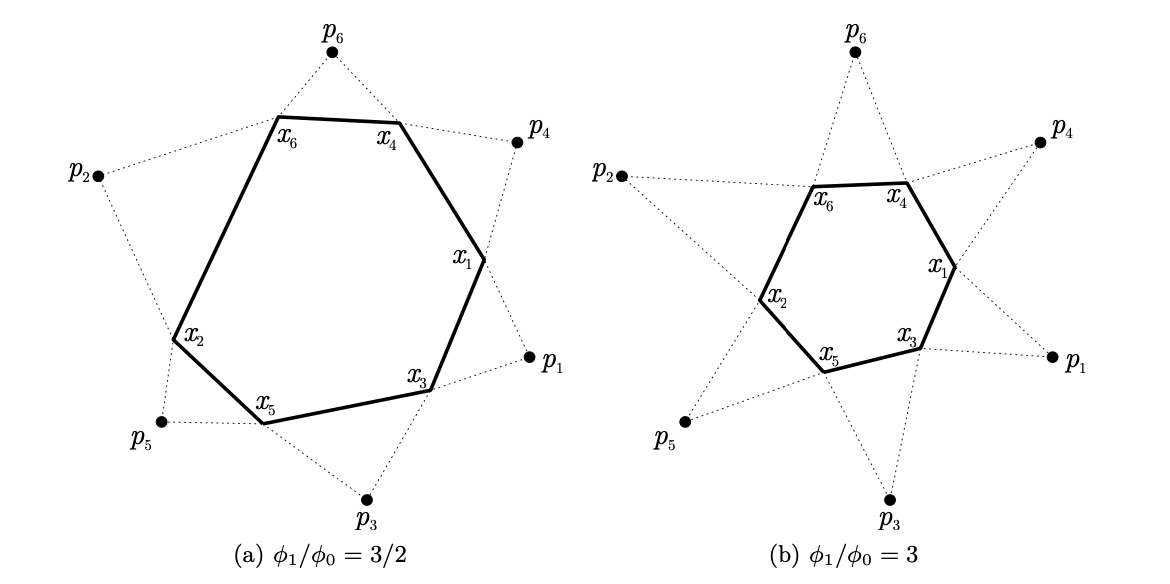
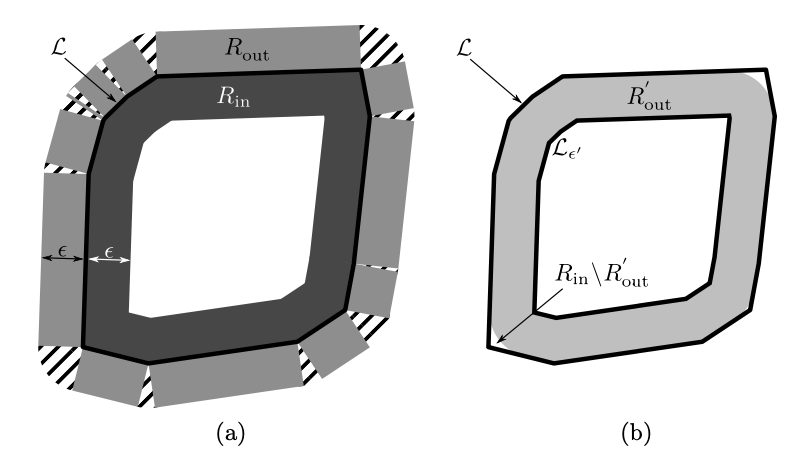
[참고] Claim9. 위의 식 (1)의 lower bound가 문제의 최적 목적 값이다. 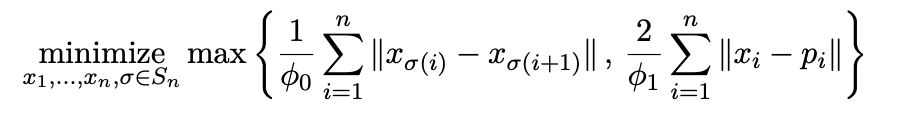
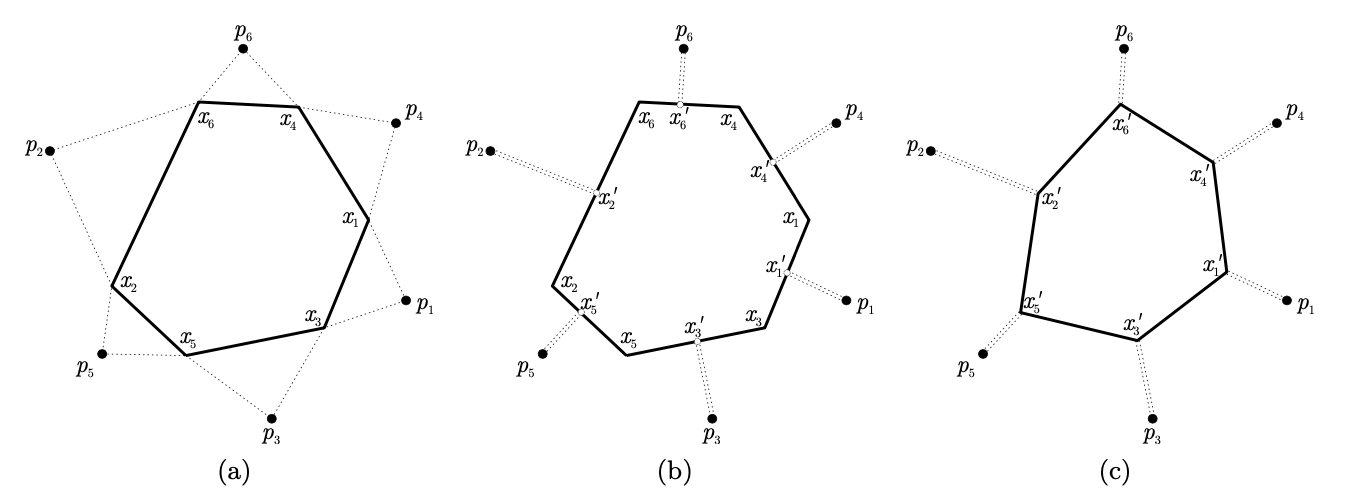
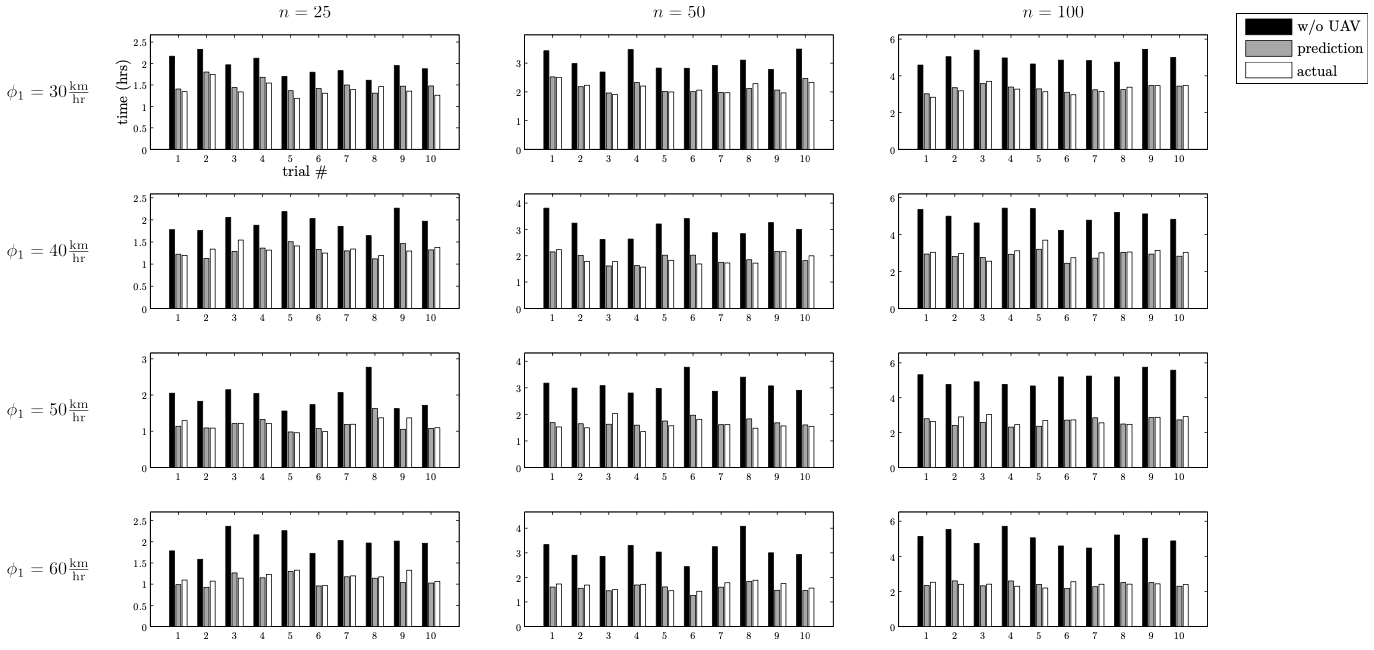
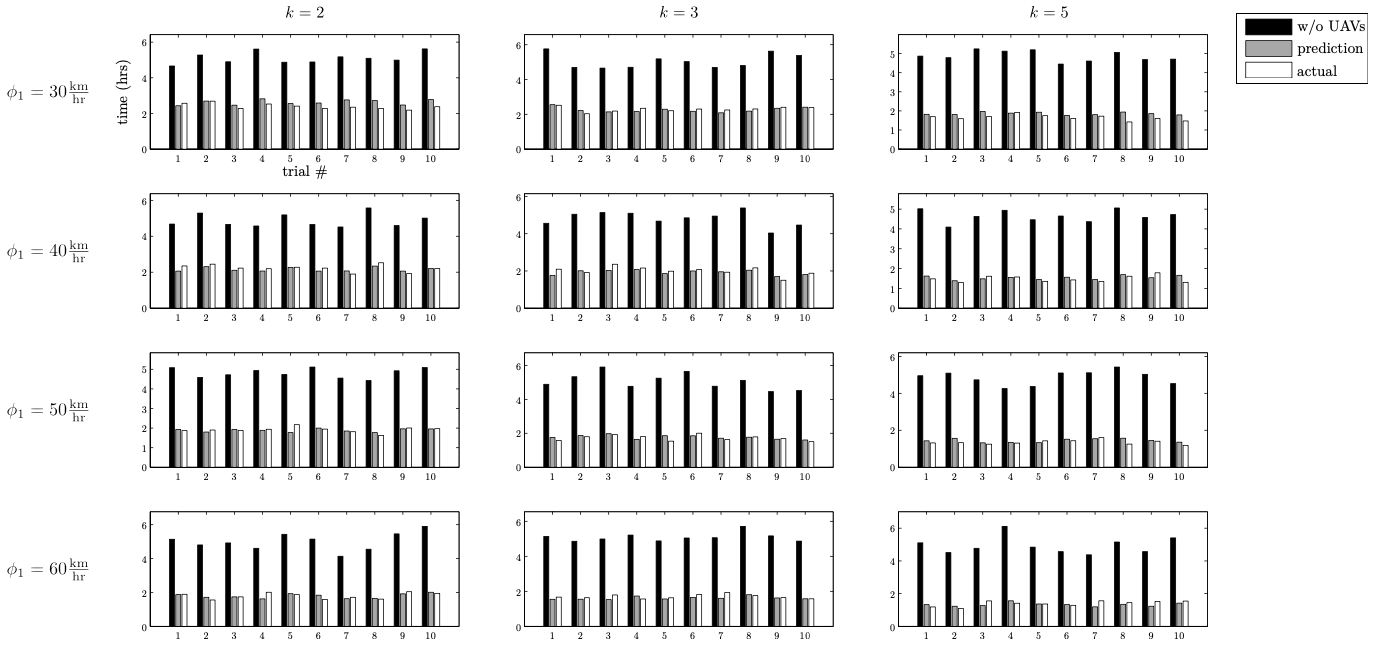
논문 결과는 다음과 같이 정리할 수 있다.
- 무인항공기와 트럭 배달의 효율성은 각각의 속도 비율의 제곱근에 비례한다.
- True globally 최적 솔루션이 아니라 트럭과 무인항공기 사이의 조정된 경로를 계산하기 위해 휴리스틱한 방법을 사용함.(분석의 weak point 중 하나)
- 이 논문에서 제시된 문제에 대한 솔루션을 찾는 테크닉을 현재까지 알지 못하지만, 물류에 대한 무인항공기의 관심이 증가함에 따라 향후 몇 년 내에 그러한 기술들이 가능할 것으로 예상함.
Cite
Carlsson, J. G., & Song, S. (2018). Coordinated logistics with a truck and a drone. Management Science, 64(9), 4052-4069. 논문 링크