Abstract
Context : The Vehicle Routing Problem (VRP) has numerous applications in real life. It clarifies in a wide area of transportation and distribution such as transportation of individuals and items, conveyance service and garbage collection. Thus, an appropriate selecting of vehicle routing has an extensive influence role to improve the economic interests and appropriateness of logistics planning.
Problem : In this study the problem is as follows: Universiti Tenaga Nasional (UNITEN) has eight buses which are used for transporting students within the campus. Each bus starts from a main location at different times every day. The bus picks up students from eight locations inside the campus in two different routes and returns back to the main location at specific times every day, starting from early morning until the end of official working hours, on the following conditions: Every location will be visited once in each route and the capacity of each bus is enough for all students included in each route.
Objectives : Our paper attempt to find an optimal route result for VRP of UNITEN by using genetic algorithm. To achieve an optimal solution for VRP of UNITEN with the accompanying targets: To reduce the time consuming and distance for all paths. which leads to the speedy transportation of students to their locations, to reduce the transportation costs such as fuel utilization and additionally the vehicle upkeep costs, to implement the Capacitated Vehicle Routing Problem (CVRP) model for optimizing UNITEN’s shuttle bus services. To implement the algorithm which can be used and applied for any problems in the like of UNITEN VRP.
Approach : The Approach has been presented based on two phases: firstly, find the shortest route for VRP to help UNITEN University reduce student’s transportation costs by genetic algorithm is used to solve this problem as it is capable of solving many complex problems; secondly, identify The CVRP model is implemented for optimizing UNITEN shuttle bus services.
Finding : The findings outcome from this study have shown that: (1) A comprehensive listed of active GACVRP; (2) Identified and established an evaluation criterion for GACVRP of UNITEN; (3) Highlight the methods, based on hybrid crossover operation, for selecting the best way (4) genetic algorithm finds a shorter distance for route A and route B. The proportion of reduction the distance for each route is relatively short, but the savings in the distance becomes greater when calculating the total distances traveled by all buses daily or monthly. This applies also to the time factor that has been reduced slightly based on the rate of reduction in the distances of the routes.
Keywords : Genetic algorithm; Vehicle routing problem; Capacitated vehicle routing problem; Optimal solution
Problem : In this study the problem is as follows: Universiti Tenaga Nasional (UNITEN) has eight buses which are used for transporting students within the campus. Each bus starts from a main location at different times every day. The bus picks up students from eight locations inside the campus in two different routes and returns back to the main location at specific times every day, starting from early morning until the end of official working hours, on the following conditions: Every location will be visited once in each route and the capacity of each bus is enough for all students included in each route.
Objectives : Our paper attempt to find an optimal route result for VRP of UNITEN by using genetic algorithm. To achieve an optimal solution for VRP of UNITEN with the accompanying targets: To reduce the time consuming and distance for all paths. which leads to the speedy transportation of students to their locations, to reduce the transportation costs such as fuel utilization and additionally the vehicle upkeep costs, to implement the Capacitated Vehicle Routing Problem (CVRP) model for optimizing UNITEN’s shuttle bus services. To implement the algorithm which can be used and applied for any problems in the like of UNITEN VRP.
Approach : The Approach has been presented based on two phases: firstly, find the shortest route for VRP to help UNITEN University reduce student’s transportation costs by genetic algorithm is used to solve this problem as it is capable of solving many complex problems; secondly, identify The CVRP model is implemented for optimizing UNITEN shuttle bus services.
Finding : The findings outcome from this study have shown that: (1) A comprehensive listed of active GACVRP; (2) Identified and established an evaluation criterion for GACVRP of UNITEN; (3) Highlight the methods, based on hybrid crossover operation, for selecting the best way (4) genetic algorithm finds a shorter distance for route A and route B. The proportion of reduction the distance for each route is relatively short, but the savings in the distance becomes greater when calculating the total distances traveled by all buses daily or monthly. This applies also to the time factor that has been reduced slightly based on the rate of reduction in the distances of the routes.
Keywords : Genetic algorithm; Vehicle routing problem; Capacitated vehicle routing problem; Optimal solution
Summary
이 논문은 유전 알고리즘을 이용해 UNITEN의 CVRP에 대한 최적의 경로 결과를 찾는다. 각 경로의 거리 감소 비율은 상대적으로 작지만, 모든 버스가 매일 또는 매월 운행하는 총 거리에 대한 절약량은 더 커진다.
본문 내용
VRP(Vehicle Routing Problem)는 실생활에서 다양한 응용분야가 있으며 그중 운송(물류) 분야에 적용이 많이 된다. 이 논문에서는 UNITEN(Universiti Tenaga Nasional)의 셔틀버스 운행에 관한 CVRP (Capacitated Vehicle Routing Problem) 문제를 유전알고리즘을 사용하여 푼다. 8개의 버스가 운행되고 main location에서 매일 다른 시간에 출발한다. 버스는 8개의 다른 location에서 2개의 다른 경로로 학생들을 픽업하고 main location으로 돌아온다. 모든 location은 각 경로에서 한번 방문되고 버스는 모든 학생을 태우기에 충분한 capacity를 가진다고 가정한다.
이 논문에서는 UNITEN CVRP의 optimal solution을 얻기 위해 다음을 목표로 한다.
그래프 Gr은 다음과 같이 표현된다. S는 station 집합, D는 station 사이의 거리를 의미한다. $$Gr = (S,D); S = {s_0,s_1,...,s_n}, D = {(s_x,s_y):s_x,s_y \in S, x < y} $$ $z$개의 차량에 대해 Decision factor function이 다음과 같이 rout 옵션을 결정한다. $$ D f(x, y, z)\left\{\begin{array}{ll}1, & \text { true } \longleftarrow \operatorname{arc}(x, y) \\ & 0, \quad \text { otherwise }\end{array}\right. $$ $z$는 경로의 거리를 줄이기 위해 1로 가정하고 CVRP를 formulation 한다. $$ \text { Minimize }=\left(\sum_{x=0, x \neq y}^{n} D_{x, y} D f_{x, y}\right) \\ \text {Therefore } x=0, y=1 \text { are subject to:} \\ Df_{x,y} = 1, \quad \forall x \in S \\ Df_{x,y} = 1, \quad \forall y \in S \\ f(x) = 100 / \sum_{x=0,y=1}^n D_{x,y} $$ 모든 path에 대한 최소 비용은 거리에 의존하기 때문에 염색체(chromosome)의 fitness value를 높이기 위해 거리를 줄여야 한다. 위의 $f(x)$는 fitness를 의미한다. (CVRP 모델이 이상하다..)
이러한 CVRP모델을 푸는 유전알고리즘 과정은 다음과 같다.
모집단 (Population)
모집단은 랜덤하게 생성된다. 각각의 염색체(chromosome)는 하나의 유효한 경로(route)를 나타내고 각 location은 유전자(gene)에 해당한다. 초기 모집단인 첫번째 염색체는 다음과 같이 표현된다. $$ 1\quad 2\quad 3\quad 4\quad 5\quad 6\quad 7\quad 8\quad 9 $$ 초기 염색체가 생성되면 적합도(fitness)가 계산되고 가장 좋은 염색체로 설정된다.
적합치 (Fitness values)
UNITEN CVRP에서 모든 path의 최소 비용은 거리에 의존한다. 염색체의 적합도는 모든 path에 대한 총 거리를 구하여 계산할 수 있다. path 거리는 D1 = station 1에서 stop 2 , D2 = station 2에서 stop 5까지의 거리 등 축약해서 나타낸다. 염색체 적합도를 높이기 위해 거리를 줄여야하고 적합도는 (100/총 거리의 합)으로 나타낸다.
선택 (Selection)
Strong selective factor는 혼합(hybrid) 교차를 위한 최적의 염색체만을 선택하여 가장 이상적인 솔루션을 유도할 수 있다. 이는 유전 알고리즘을 빨리 끝낼 수 있게 한다. 반면 Weak selective factor는 혼합 교차에서 적합도가 낮은 솔루션까지 확인해야함으로 더 많은 시간이 걸린다. 기존의 룰렛 휠(roulette wheel)은 가장 높은 적합도를 가지는 염색체를 선택하여 새로운 염색체를 만들고 이를 복제하여 새로운 세대(generation)를 형성하는 염색체 선택 방식이다.
교차 (Crossover)
랜덤 벡터를 생성하여 유전자를 선택하는 혼합교차가 이 알고리즘에서 사용되었다. 1이면 primary parent에서 0이면 second parent의 유전자를 선택하고 이를 결합하여 자손을 만든다. 예를 들어 부모 C1과 C2가 다음과 같이 주어지고 이진 벡터가 [10101001]이라면 자손1이 다음과 같이 생성된다.
유전 알고리즘 연산을 계속 진행하면 local optimum에 도달하게 되는데 새로운 염색체에 확률적으로 돌연변이를 발생시켜 local optimum에서 빠져나올 수 있도록 한다. 돌연변이 체계는 모든 루프에서 3가지 상황을 반복한다. 첫 번째 염색체의 대체 염색체를 생성하며 테스트하고 두 개의 결과 유전자 사이에 immediate route가 없으면 새로운 염색체는 무효가 된다. 만약 새로운 염색체가 좋다면 적합도 함수 값이 계산된다. 만약 적합도 함수 값이 기존보다 우수하면 새로운 염색체가 best가 되고 루프가 종료된다.
결과 (Results)
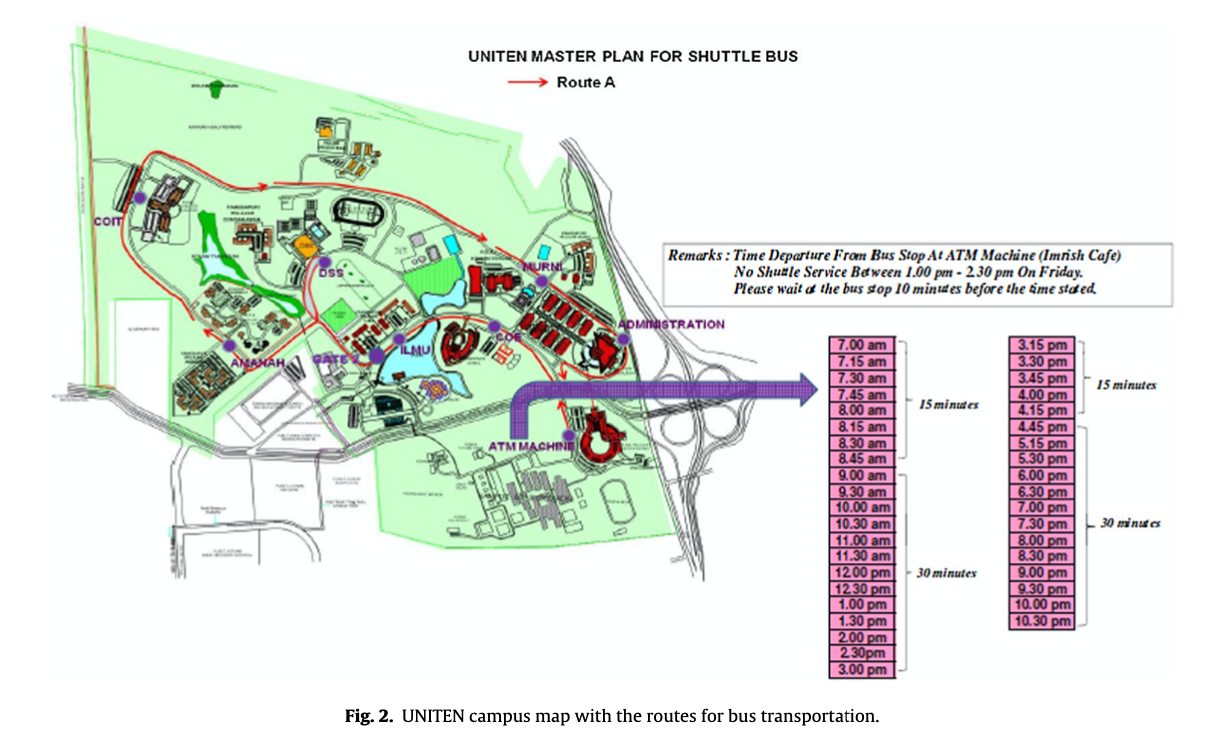
이 연구는 UNITEN에서 학생들의 총 교통비를 줄이는 것을 목표로 하며 비용은 주로 경로의 거리에 관한 것이다. 향상된 유전 알고리즘은 테스트와 검증을 통해 station 양에 가장 적합한 경로를 찾는 것이 입증되었다. 버스는 학생들을 수송하기 위해 매일 A와 B 두 개의 경로로 운행된다.
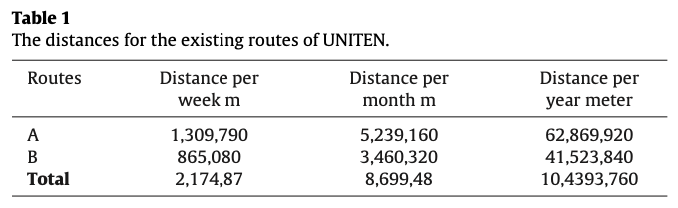
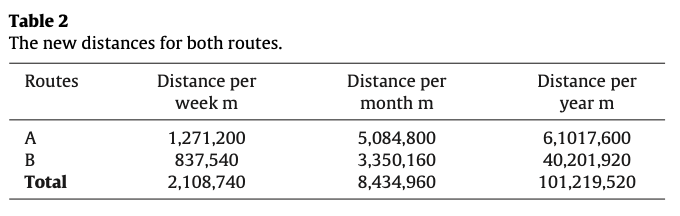
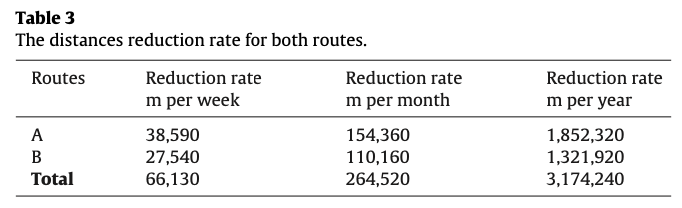
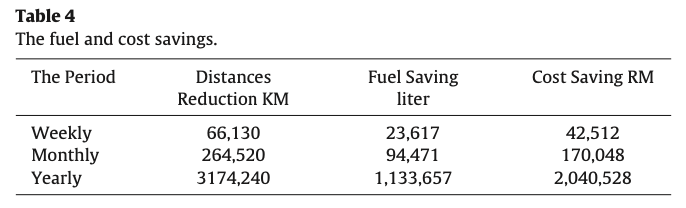Table 1은 기존 경로의 거리를 나타내고 Table 2는 새로운 경로의 거리를 나타낸다. Table 3은 이 둘의 차이를 나타내고 Table 4는 거리 감소에 대한 비용 절약정도를 나타낸다.
각 경로의 거리 감소 정도는 작지만 두 경로에 대한 장기적인 감소는 크다. 알고리즘의 성능과 신뢰성을 검증하기 위해 UKM의 동일한 문제를 풀기 위해 적용되었고 더 짧은 경로를 찾는데 성공하였다. UKM 각 경로의 거리 감소는 꽤 크다.
논문의 결론은 다음과 같이 정리할 수 있다.
Mohammed, M. A., Ghani, M. K. A., Hamed, R. I., Mostafa, S. A., Ahmad, M. S., & Ibrahim, D. A. (2017). Solving vehicle routing problem by using improved genetic algorithm for optimal solution. Journal of Computational Science, 21, 255-262. 논문 링크
이 논문에서는 UNITEN CVRP의 optimal solution을 얻기 위해 다음을 목표로 한다.
- 모든 path에 대한 시간 소모와 거리를 줄이는 것 (빠른 수송을 가능하게 함)
- 연료 사용과 추가적인 차량 유지 비용 등의 운송 비용을 줄이는 것
- UNITEN의 셔틀 버스 서비스를 최적화하는 CVRP 모델을 구현하는 것
- UNITEN CVRP와 같은 문제에 적용될 수 있는 알고리즘을 구현하는 것
그래프 Gr은 다음과 같이 표현된다. S는 station 집합, D는 station 사이의 거리를 의미한다. $$Gr = (S,D); S = {s_0,s_1,...,s_n}, D = {(s_x,s_y):s_x,s_y \in S, x < y} $$ $z$개의 차량에 대해 Decision factor function이 다음과 같이 rout 옵션을 결정한다. $$ D f(x, y, z)\left\{\begin{array}{ll}1, & \text { true } \longleftarrow \operatorname{arc}(x, y) \\ & 0, \quad \text { otherwise }\end{array}\right. $$ $z$는 경로의 거리를 줄이기 위해 1로 가정하고 CVRP를 formulation 한다. $$ \text { Minimize }=\left(\sum_{x=0, x \neq y}^{n} D_{x, y} D f_{x, y}\right) \\ \text {Therefore } x=0, y=1 \text { are subject to:} \\ Df_{x,y} = 1, \quad \forall x \in S \\ Df_{x,y} = 1, \quad \forall y \in S \\ f(x) = 100 / \sum_{x=0,y=1}^n D_{x,y} $$ 모든 path에 대한 최소 비용은 거리에 의존하기 때문에 염색체(chromosome)의 fitness value를 높이기 위해 거리를 줄여야 한다. 위의 $f(x)$는 fitness를 의미한다. (CVRP 모델이 이상하다..)
이러한 CVRP모델을 푸는 유전알고리즘 과정은 다음과 같다.
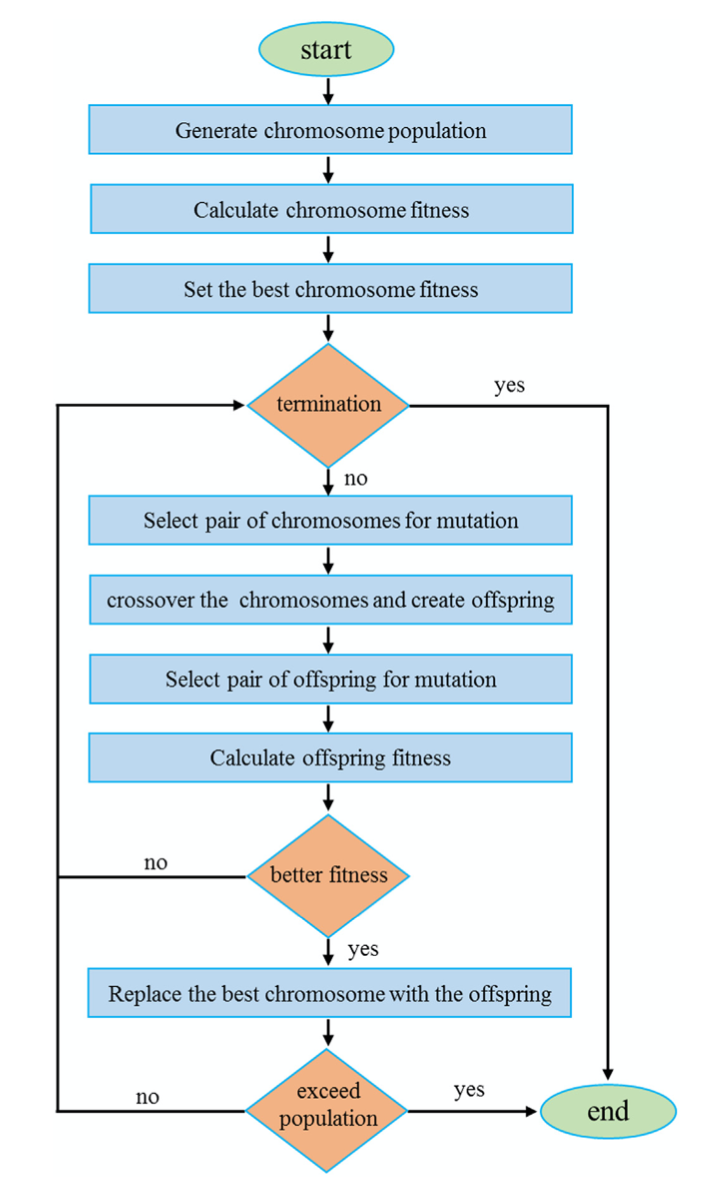
모집단 (Population)
모집단은 랜덤하게 생성된다. 각각의 염색체(chromosome)는 하나의 유효한 경로(route)를 나타내고 각 location은 유전자(gene)에 해당한다. 초기 모집단인 첫번째 염색체는 다음과 같이 표현된다. $$ 1\quad 2\quad 3\quad 4\quad 5\quad 6\quad 7\quad 8\quad 9 $$ 초기 염색체가 생성되면 적합도(fitness)가 계산되고 가장 좋은 염색체로 설정된다.
적합치 (Fitness values)
UNITEN CVRP에서 모든 path의 최소 비용은 거리에 의존한다. 염색체의 적합도는 모든 path에 대한 총 거리를 구하여 계산할 수 있다. path 거리는 D1 = station 1에서 stop 2 , D2 = station 2에서 stop 5까지의 거리 등 축약해서 나타낸다. 염색체 적합도를 높이기 위해 거리를 줄여야하고 적합도는 (100/총 거리의 합)으로 나타낸다.
선택 (Selection)
Strong selective factor는 혼합(hybrid) 교차를 위한 최적의 염색체만을 선택하여 가장 이상적인 솔루션을 유도할 수 있다. 이는 유전 알고리즘을 빨리 끝낼 수 있게 한다. 반면 Weak selective factor는 혼합 교차에서 적합도가 낮은 솔루션까지 확인해야함으로 더 많은 시간이 걸린다. 기존의 룰렛 휠(roulette wheel)은 가장 높은 적합도를 가지는 염색체를 선택하여 새로운 염색체를 만들고 이를 복제하여 새로운 세대(generation)를 형성하는 염색체 선택 방식이다.
교차 (Crossover)
랜덤 벡터를 생성하여 유전자를 선택하는 혼합교차가 이 알고리즘에서 사용되었다. 1이면 primary parent에서 0이면 second parent의 유전자를 선택하고 이를 결합하여 자손을 만든다. 예를 들어 부모 C1과 C2가 다음과 같이 주어지고 이진 벡터가 [10101001]이라면 자손1이 다음과 같이 생성된다.
유전 알고리즘 연산을 계속 진행하면 local optimum에 도달하게 되는데 새로운 염색체에 확률적으로 돌연변이를 발생시켜 local optimum에서 빠져나올 수 있도록 한다. 돌연변이 체계는 모든 루프에서 3가지 상황을 반복한다. 첫 번째 염색체의 대체 염색체를 생성하며 테스트하고 두 개의 결과 유전자 사이에 immediate route가 없으면 새로운 염색체는 무효가 된다. 만약 새로운 염색체가 좋다면 적합도 함수 값이 계산된다. 만약 적합도 함수 값이 기존보다 우수하면 새로운 염색체가 best가 되고 루프가 종료된다.
결과 (Results)
이 연구는 UNITEN에서 학생들의 총 교통비를 줄이는 것을 목표로 하며 비용은 주로 경로의 거리에 관한 것이다. 향상된 유전 알고리즘은 테스트와 검증을 통해 station 양에 가장 적합한 경로를 찾는 것이 입증되었다. 버스는 학생들을 수송하기 위해 매일 A와 B 두 개의 경로로 운행된다.
각 경로의 거리 감소 정도는 작지만 두 경로에 대한 장기적인 감소는 크다. 알고리즘의 성능과 신뢰성을 검증하기 위해 UKM의 동일한 문제를 풀기 위해 적용되었고 더 짧은 경로를 찾는데 성공하였다. UKM 각 경로의 거리 감소는 꽤 크다.
논문의 결론은 다음과 같이 정리할 수 있다.
- UNITEN의 셔틀 버스 서비스를 최적화하기 위해 CVRP 모델을 구현하고 유전 알고리즘을 활용하여 이를 해결하였다.
- 그러나 알고리즘에서 단일 변수인 거리만 고려하고 버스 정류장이 적고 한정되어 있어 솔루션을 찾기가 상당히 쉽기 때문에 복잡한 문제를 효율적으로 처리하는 것으로 알려진 유전 알고리즘의 강점을 드러내지 않았다는 한계점이 있다.
- 추후에는 Selangor와 UNITEN의 다른 locations간의 최단 거리를 찾는 알고리즘으로 확장할 것이다.
Cite
Mohammed, M. A., Ghani, M. K. A., Hamed, R. I., Mostafa, S. A., Ahmad, M. S., & Ibrahim, D. A. (2017). Solving vehicle routing problem by using improved genetic algorithm for optimal solution. Journal of Computational Science, 21, 255-262. 논문 링크