Abstract
The usual column generation model for a Vehicle Routing Problem involves an elementary shortest-path sub- problem. The worst-case complexity of the known algorithms for this problem being too high, the elementary-path constraint is usually relaxed. Indeed, as each customer must be visited exactly once, the two problems with and without the elementary-path constraint have the same optimal integer solutions. In this article, we propose one theoretical and several practical improvements to the algorithm for elementary paths. We obtain better lower bounds and pruning of the search tree, and these improvements allowed us to find an exact solution to 17 instances of the Solomon benchmark suite which were previously open.
Keywords : Vehicle routing; Branch-and-Price; Elementary shortest path;
Keywords : Vehicle routing; Branch-and-Price; Elementary shortest path;
Summary
VRP에서 보통 column generation은 elementary shortest-path를 subproblem으로 포함한다. 이 논문에서는 elementary path에 대한 알고리즘 개선을 제안한다. 더 좋은 lower bound 얻고 search tree를 pruning하여 솔로몬 데이터의 17개 인스턴스에 대한 exact solution을 찾았다.
본문 내용
이 논문에서는 Vehicle Routing Problem with Time Windows (VRPTW)를 다룬다. VRP는 exact method인 column generation을 사용하여 optimal solution을 찾을 수 있다. original linear program은 Dantzig-Wolfe decomposition을 통해 linear restricted master problem과 pricing subproblem으로 나뉜다. 마스터 문제는 이진 변수를 가지는 partitioning problem이 되고 pricing subproblem은 새로운 column 생성에 대한 제한된 최단 경로 문제가 된다.
경로에 cycle이 존재하는 Shortest Path with Resource Constraints and Time Windows (SPRCTW) column generation 모델의 optimal integer solution은 elementary routes만을 포함한다. ESPRCTW가 NP-hard인 반면에 SPRCTW는 pseudo-polynomial 알고리즘을 사용할 수 있기 때문에 이를 활용한다. 이 논문에서는 relaxed restricted master problem로 얻은 더 좋은 lower bound와 cycle 제약을 고려한 영향을 줄이기 위한 기술들을 제시한다.
여기서는 두 가지 VRP 모델을 소개한다. 각각은 VRP with TIme Windows와 최대 용량 $C_k$를 가지는 $K$개의 차량이 있는 문제이다. $N$개의 노드가 방문되어야하고 각 노드 $i$에서 quantity $q_i$가 배송되어야만 한다. 각 노드는 $[a_i,b_i]$로 정의된 time window를 가지며 $A$는 arc 집합을 나타내고 $d$는 각 arc에 대한 거리를 나타낸다. 노드 0과 $N+1$은 dummy 노드 즉, depot를 나타낸다. 목적함수는 $K$개의 차량이 모든 노드에 quantity를 배송하기 위한 최소 거리의 경로 집합를 찾는 것이다.
MIP model
$x_{ijk}$는 차량 $k$가 arc $(i,j)$ 사용에 대한 이진변수를 나타내고 $s_{ik}$는 차량 $k$가 노드 i에 도착하는 시간을 나타낸다. 제약식은 routes가 valid path를 갖도록 해준다. (모든 차량이 용량을 넘지않고 각 노드가 정확히 한번만 커버되는 것)
$$ \begin{align} \min \quad & \sum_{k=1}^{K} \sum_{(i, j) \in A} d(i, j) x_{i j k}, \\ & \sum_{j \in \delta^{+}(0)} x_{0 j k}=1 \quad \forall k \in\{1, \ldots, K\}, \\ & \sum_{i \in \delta^{-}(j)} x_{i j k}-\sum_{i \in \delta^{+}(j)} x_{j i k}=0 \quad \forall k \in\{1, \ldots, K\}, \quad \forall j \in\{1, \ldots, N\}, \\ & \sum_{i \in \delta^{-}(N+1)} x_{i, N+1, k}=1 \quad \forall k \in\{1, \ldots, K\}, \\ & \sum_{i \in S} \sum_{j \in S, j \neq i} x_{i j k} \leqslant|S|-1 \quad \forall k \in\{1, \ldots, K\}, \quad \forall S \subset X , 1<|S|< N, \\ & \sum_{k=1}^{K} \sum_{j \in \delta^{+}(i)} x_{i j k}=1 \quad \forall i \in\{1, \ldots, N\}, \\ & \sum_{i=1}^{N} q_{i} \sum_{j \in \delta^{+}(i)} x_{i j k} \leqslant C_{k} \quad \forall k \in\{1, \ldots, K\}, \\ & s_{i k}+d(i, j)-K\left(1-x_{i j k}\right) \leqslant s_{j k} \quad \forall(i, j) \in A, \quad \forall k \in\{1, \ldots, K\}, \\ & \quad \quad \quad a_{i} \leqslant s_{i k} \leqslant b_{i} \quad \forall i \in\{1, \ldots, N\}, \quad \forall k \in\{1, \ldots, K\}, \\ & \quad \quad \quad x_{ijk} \in \{0,1\} \quad \forall k \in \{1, \ldots, K\}, \quad \forall (i,j) \in A. \end{align} $$
목적함수(1)는 사용하는 arc의 거리 총합을 최소화하는 것이다. 제약식(2)-(4)는 차량 $k$의 flow를 나타내고 제약식(5)는 subtour를 제거해준다. 제약식(6)은 각 노드가 최대 한개의 차량에 의해 방문되어야함을 뜻하고 제약식(7)은 차량의 용량을 넘지않아야함을 뜻한다. 제약식(8)과 (9)는 time windows를 정의한다. 이 때 subtour 제약식의 수가 exponential이므로 Branch-and-Cut을 사용하여 dynamically 추가해준다.
Dantzig-Wolfe decomposition
위에서 정의한 MIP 모델에 Dantzig-Wolfe decomposition이 적용된다. 주어진 $k$에 대한 제약식(2)-(5)와 (7)에 해당하는 행렬 $B_k$를 고려한다. $B_k$로 정의된 polytope은 차량 $k$에 대한 valid path의 extreme points 집합 $\Omega_k$를 허용한다. 따라서 그 포인트 중 하나를 path들의 linear combination으로 쓸 수 있다. 이를 위해 극점 $\lambda^p_k$에 해당하는 path에 속하면 1 아니면 0인 계수 $x^p_{ijk}$를 사용한다. 따라서 $k \in \{1,\ldots,K\}$에 대해 솔루션 $x_{ijk}$를 다음과 같이 나타낼 수 있다.
$$ \begin{aligned} &x_{ijk} = \sum_{p \in \Omega_k} x^p_{ijk} \lambda^p_k \quad \forall (i,j) \in A, \\ &\sum_{p \in \Omega_k} \lambda^p_k = 1 \quad \forall k \in \{1,\ldots,K\}, \\ &\lambda^p_k \geqslant 0 \quad \forall p \in \Omega_k. \end{aligned} $$
차량 $k$에 대한 route $p$의 cost를 $c^p_k$로 정의힌다. 또한 양수인 정수 $a^p_{ik}$는 route $p$에 대해 차량 $k$가 노드 $i$를 방문한 횟수를 나타낸다.
$$ \begin{aligned} &c^p_k = \sum_{(i,j) \in A} c(i,j)x^p_{ijk} \quad \forall k \in \{1,\ldots,K\}, \quad \forall p \in \Omega_k, \\ &a^p_{ik} = \sum_{j \in \delta^+(i)} x^p_{ijk} \quad \forall i \in \{1,\ldots,\}N \quad \forall k \in \{1,\ldots,\}K, \quad \forall p \in \Omega_k, \end{aligned} $$
이러한 표현들을 원래 모델로 대체한다면 다음과 같은 decomposed model을 얻는다.
$$ \begin{aligned} \min \quad & \sum_{k=1}^{K} \sum_{p \in \Omega_k} c^p_k \lambda^p_k, \\ &\sum_{k=1}^{K} \sum_{p \in \Omega_k} a^p_{ik} \lambda^p_k = 1 \quad \forall i \in \{1,\ldots,N\}, \\ &\sum_{p \in \Omega_k} \lambda^p_k = 1 \quad \forall k \in \{1,\ldots,K\}, \\ &\lambda^p_k \geqslant 0 \quad \forall k \in \{1,\ldots,K\} \forall p \in \Omega_k. \end{aligned} $$
capacity, subtour elimination, time window 제약은 extreme point path의 validity를 정의하는 subproblems로 이동된다.
$$ \begin{aligned} \min \quad & \sum_{(i, j) \in A} d(i, j) x_{i j}, \\ & \sum_{j \in \delta^{+}(0)} x_{0 j }=1 , \\ & \sum_{i \in \delta^{-}(j)} x_{i j}-\sum_{i \in \delta^{+}(j)} x_{j i}=0 \quad \forall j \in\{1, \ldots, N\}, \\ & \sum_{i \in \delta^{-}(N+1)} x_{i, N+1}=1 , \\ & \sum_{i \in S} \sum_{j \in S, j \neq i} x_{i j} \leqslant|S|-1 \quad \forall S \subset X , 1<|S|< N, \\ & \sum_{i=1}^{N} q_{i} \sum_{j \in \delta^{+}(i)} x_{i j } \leqslant C_{k}, \\ & s_{i }+d(i, j)-K\left(1-x_{i j }\right) \leqslant s_{j } \quad \forall(i, j) \in A, \\ & \quad \quad \quad a_{i} \leqslant s_{i} \leqslant b_{i} \quad \forall i \in\{1, \ldots, N\}, \\ & \quad \quad \quad x_{ij} \in \{0,1\} \quad \forall (i,j) \in A. \end{aligned} $$ Identical vehicles
차량이 동일할 때 (총 용량이 같을 때) 모델의 일부를 다음과 같이 바꿀 수 있다. $$ \begin{aligned} \lambda^p = \sum^K_{k=1} \lambda^p_k \quad \forall p \in \Omega = \bigcup^K_{k=1} \Omega_k \end{aligned} $$ 그러면 다음과 같은 모델을 얻을 수 있다. $$ \begin{align} \min \quad & \sum_{p \in \Omega} c^p \lambda^p, \notag \\ &\sum_{p \in \Omega} a^p_{i} \lambda^p = 1 \quad \forall i \in \{1,\ldots,N\}, \\ &\sum_{p \in \Omega} \lambda^p = K, \notag \\ & \quad \quad \lambda^p \geqslant 0 \quad \forall p \in \Omega. \end{align} $$
decomposed model은 가능한 path 변수를 매우 많이 포함한다. 만약 $N$이 노드의 수라면 이론적으로 path 변수의 수는 $N$!개로 증가할 수 있다. 그렇기 때문에 column generation을 사용한다.
Branch-and-Price는 흔히 사용되는 branching 기법이다. column generation을 할 때 reduced cost를 확인하여 제한된 모델에 추가될 새로운 변수를 찾는데 이러한 과정을 pricing이라 한다. 더 이상 추가할 column이 없을 때까지 반복하며 변수가 fractional인 경우에는 branching을 해준다. 일반적으로 set partitioning 제약식(11)은 set covering 제약으로 바뀐다.
The pricing scheme
$\pi_i$와 $\pi_0$을 각각 제약식 (11)과 (12)에 대한 dual 이라고 한다면 reduced cost는 다음과 같다. $$ \begin{aligned} rc(p) = c(p) - \sum^N_{i=1} a^p_i \pi_i - \pi_0 = \sum_{(i,j) \in p} (d(i,j)-\pi_j) - \pi_0 \end{aligned} $$
따라서 subproblem은 다음과 같은 cost를 가지고 용량을 넘지 않는 the shortest elementary path를 찾는 문제가 된다. $$ \begin{aligned} &rc(i,j) = d(i,j)-\pi_j \quad \forall j \in \{1,\ldots,N\}, \\ &rc(i,N+1) = -\pi_0. \end{aligned} $$
Various possible subproblems
path $p = (i_0 = 0, i_1, \ldots, (N+1))$라 하자. resources는 $L$로 일반화 될 수 있고 $l$에 의해 인덱싱된다. $D^l_i$는 노드 $i$에서 resource $l$의 누적된 양을 나타낸다. 거리 함수 $d^l(i,j)$는 $i$와 $j$사이의 resource $l$의 누적을 정의한다. $[a^l_i,b^l_i]$는 resource와 노드 각각의 쌍으로 정의된다. 여기서는 두 개의 연속적인 노드 $i$와 $j$ 사이의 누적된 resource의 증가는 triangle inequality를 만족해야한다는 것을 이용한다. $$ \begin{aligned} d^l(i,k) \leqslant d^l(i,j) + d^l(j,k) \quad \forall l = 1\ldots L. \end{aligned} $$
Theorem 1. triangle inequality에 대한 resource 누적과 노드 사이의 cost 누적이 strictly positive일 때, non-elementary path를 가지는 마스터 문제의 optimal integer solution은 elementary path만을 포함한다.
일반적으로 최단경로 서브문제는 cycle이 허용되는 pseudo-polynomial labeling algorithm으로 풀린다. 그러나 elementary path만 사용된다면 relaxed 마스터 문제는 더 제한되고 더 좋은 bound가 제공될 것이다.
Labeling algorithm
노드 $i$에서 partial path $p$는 label $E_p = (rc_p, D^0_p, \ldots , D^L_p)$와 관련되어 있다. 레이블링 알고리즘에서 사용되는 기본적인 rule은 dominance rule이고 다음을 만족하면 partial path $p_1$은 다른 partial path $p_2$를 dominate한다. $$ \begin{align} &rc_1 \leqslant rc_2, \\ &D^l_1 \leqslant D^l_2 \quad \forall l \in \{0,\ldots L\} \end{align} $$ dominance rule은 elementary shortes path에 직접적으로 사용될 수 없다. 따라서 이 논문의 중점은 실질적이고 효율적인 알고리즘의 수정을 제안하는 것이다.
이 논문에서는 Ryan-Foster rules에 기초한 branching 기법을 사용한다. 같은 node $i$와 $j$를 공유하는 두 개의 fractional routes를 찾는다. (한 경로는 arc $(i,j)$를 사용하고 다른 경로는 사용하지 않는다.) 각 branch에서 최단 경로 서브문제는 문제의 구조를 깨지 않고 쉽게 수정될 수 있다.
좋지 않은 lower bound를 가지는 노드를 prune하기 위해 bound의 quality가 중요한데 이 논문에서는 relaxation의 quality를 향상하기 위한 두 가지 방법을 제시한다. 첫 번째는 relaxation에 cutting plane을 추가하는 것이고 두 번째는 elementary shortest path subproblem에 기초한 것이다. SPRCTW를 사용할 경우 마스터 문제를 MP로 표시하고 ESPRCTW를 사용할 경우 EMP로 표시한다. MP에서 통합 제약을 제거하면 RMP로 표시하고 EMP에서 제거하면 REMP로 표시한다.
Simple example
depot에서 매우 먼 두 개의 노드 $i$와 $j$를 가지는 문제에 대해 다음과 같이 가정한다. $$ \begin{aligned} &d(0,i) = d(0,j) = 100,\\ &d(i,j) == 1. \end{aligned} $$ 용량과 time window는 크다고 가정한다. EMP의 optimal relaxed solution은 $LB_{elem}$ = 201 이 되도록 unique route 0-$i$-$j$-$(N+1)$로 만들어 진다. cycles가 허용되면 0-$(i-j)^n$-($N$+1)의 route 형식으로 $i$-$j$가 $n$번 반복된다.
relaxed problem으로 부터 얻은 솔루션을 향상시키는 가장 흔한 방법은 $k$-path cuts과 같은 cutting plane을 추가하는 것이다. $S$를 노드 집합, $\delta(S)$를 $S$에서의 outgoing arcs의 집합 ($\delta(S)$ = {($i$,$j$ $\in$ $A$/ $i$ $\in$ $S$, $j$ $\notin$ $S$}), $\mu^p_S$를 path $p$가 $\delta(S)$에서 가지는 arcs의 수라고 하자. 어떤 $k$ $\leqslant$ $\kappa(S)$에 대해 그 집합에서 최소 한개의 노드를 포함하는 경로에 해당하는 변수 $\lambda$에 $k$-path cut으로 알려진 새로운 제약을 다음과 같이 추가할 수 있다. $$ \begin{aligned} \sum_{p \in \Omega} \mu^p_S \lambda^p \geqslant k. \end{aligned} $$ cut을 추가하는 것은 lower bound를 향상 시킬 수 있다. 그러나 MP에 subtour cut을 추가하여 얻은 bound는 EMP에서 얻은 bound와 같지 않다. 예를 들어 세 개의 노드 $i$, $j$, $k$를 가지고 있다고 가정하면 경로의 집합은 각각 $ \frac{1}{2}$의 값을 가질 수 있다.
0-$j$-$k$-($N$+1),
0-$i$-$j$-$k$-$i$-($N$+1).
이 솔루션이 어떤 subtour cut을 위반하지 않더라도 cycle을 포함하여 EMP의 솔루션이 될 수 없을 것이다. ESP가 풀기 더 어렵지만 cutting plane을 사용할 때 relaxation에 추가되는 violated cut을 분리하기 위해 다른 복잡한 알고리즘을 사용해야만 한다.
Use of elementary paths
MP와 EMP의 제약조건이 동일하고 column 집합이 다른 하나에 포함되어 있으면 MP는 EMP의 relaxation이고 RMP는 REMP의 relaxation이다. 따라서 서브문제에 ESPRCTW를 사용한다. 알고리즘의 worst practical efficiency와 better quality of bounds 사이에서 적절한 타협점을 갖도록 한다.
elementary path 문제에 대한 labeling algorithm의 수정에 대해 제안하는데 두 개의 주요한 차이점이 적용된다.
A preliminary modified dominance rule
수정된 지배 규칙은 부분 경로 $p_1$이 다른 부분 경로 $p_2$를 지배하는 충분 조건이 (13)과 (14) 조건을 만족하고 노드 집합 $V(p_2)$에 $V(p_1)$을 포함할 때 사용된다. $$ \begin{align} V(p_1) \subseteq V(p_2). \end{align} $$ 기본적인 새로운 지배 규칙은 많은 레이블을 만들어낼 것이다. 실제로 노드의 집합이 다른 것에 포함되지 않는((15)를 만족하지 않는) 두 개의 부분 경로는 지배 규칙에 해당되지 않는다. 따라서 이 규칙에 대한 complete 수정과 heuristic 수정에 대한 개선을 소개한다.
Exact improvement of the dominance rule
$p_1$의 일부 노드를 거치면서 얻을 수 있는 reduced cost의 예상되는 개선을 추정함으로써 지배 규칙을 향상시킬 수 있다. $p_1$과 $p_2$를 같은 노드 $m$에서 끝나는 두 개의 부분 경로라고 하자. $V(p)$는 부분 경로 $p$에 의해 방문된 노드의 집합이다. $V(p_1)$ \ $V(p_2)$ = {n}일 때 근사치를 고려해보자.
1. Bound on improvement with $\pi_n$ : $p^*_2$가 부분 경로 $p_2$의 확장이기 때문에 $n$을 제외하고 $p^*_1$을 같은 방법으로 만들 수 있다. $p^*_2$에서 이전 노드 $i$와 다음 노드 $j$를 사용하여 다음과 같이 나타낼 수 있다. $$ \begin{aligned} rc^*_2 - rc^*_1 = c(i,n) + c(n,j) - c(i,j) - \pi_n + rc_2 -rc_1. \end{aligned} $$ 따라서 다음과 같은 경우에만 $p^*_2$가 $p^*_1$보다 더 좋다. $$ \begin{aligned} c(i,n) + c(n,j) - c(i,j) - \pi_n + rc_2 -rc_1 < 0. \end{aligned} $$ 비용 부분(triangle inequality로 인해 항상 양수이다)을 과소평가함으로써 $p_2$를 제거하기 위한 충분 조건은 다음과 같다. $$ \begin{align} - \pi_n \geqslant rc_1 -rc_2. \end{align} $$ 2. Bounds on improvement with $\pi_n$ − $minAddedArcCost_n$: 비용 부분의 더 나은 근사를 사용하고 다음과 같은 식을 사용하여 과소평가 한다. $$ \begin{align} minAddedArcCost_n = min_{i\in prec(n),j\in succ(n)}(c(i, n) + c(n, j) − c(i, j)), \end{align} $$ $prec(n)$은 노드 $n$의 가능한 predecessors의 집합, $succ(n)$은 가능한 successors의 집합이다. 이는 각 노드 $n$에 대한 알고리즘 초기화 단계에서 계산될 수 있다. 따라서 충분 조건은 다음과 같다. $$ \begin{align} minAddedArcCost_n - \pi_n \geqslant rc_1 - rc_2. \end{align} $$ (16)과 (17) 두 개의 조건은 더 많은 레이블을 파악하는데 사용될 수 있다. 이러한 조건들은 $Card(V(p_1)$\ $V(p_2))$ > 1인 경우에 일반화 될 수 있다. 그러나 좋은 bound를 찾는 것이 어렵기 때문에 알고리즘을 $Card(V(p_1)$\ $V(p_2))$ $\leqslant$ 2인 경우로 제한했다.
Computational Results
데이터는 Solomon을 사용한다. Table 1에서는 R1과 RC1에서 얻은 bound를 [11]과 비교한다.
논문의 결론은 다음과 같이 정리할 수 있다.
Chabrier, A. (2006). Vehicle routing problem with elementary shortest path based column generation. Computers & Operations Research, 33(10), 2972-2990. 논문 링크
경로에 cycle이 존재하는 Shortest Path with Resource Constraints and Time Windows (SPRCTW) column generation 모델의 optimal integer solution은 elementary routes만을 포함한다. ESPRCTW가 NP-hard인 반면에 SPRCTW는 pseudo-polynomial 알고리즘을 사용할 수 있기 때문에 이를 활용한다. 이 논문에서는 relaxed restricted master problem로 얻은 더 좋은 lower bound와 cycle 제약을 고려한 영향을 줄이기 위한 기술들을 제시한다.
여기서는 두 가지 VRP 모델을 소개한다. 각각은 VRP with TIme Windows와 최대 용량 $C_k$를 가지는 $K$개의 차량이 있는 문제이다. $N$개의 노드가 방문되어야하고 각 노드 $i$에서 quantity $q_i$가 배송되어야만 한다. 각 노드는 $[a_i,b_i]$로 정의된 time window를 가지며 $A$는 arc 집합을 나타내고 $d$는 각 arc에 대한 거리를 나타낸다. 노드 0과 $N+1$은 dummy 노드 즉, depot를 나타낸다. 목적함수는 $K$개의 차량이 모든 노드에 quantity를 배송하기 위한 최소 거리의 경로 집합를 찾는 것이다.
MIP model
$x_{ijk}$는 차량 $k$가 arc $(i,j)$ 사용에 대한 이진변수를 나타내고 $s_{ik}$는 차량 $k$가 노드 i에 도착하는 시간을 나타낸다. 제약식은 routes가 valid path를 갖도록 해준다. (모든 차량이 용량을 넘지않고 각 노드가 정확히 한번만 커버되는 것)
$$ \begin{align} \min \quad & \sum_{k=1}^{K} \sum_{(i, j) \in A} d(i, j) x_{i j k}, \\ & \sum_{j \in \delta^{+}(0)} x_{0 j k}=1 \quad \forall k \in\{1, \ldots, K\}, \\ & \sum_{i \in \delta^{-}(j)} x_{i j k}-\sum_{i \in \delta^{+}(j)} x_{j i k}=0 \quad \forall k \in\{1, \ldots, K\}, \quad \forall j \in\{1, \ldots, N\}, \\ & \sum_{i \in \delta^{-}(N+1)} x_{i, N+1, k}=1 \quad \forall k \in\{1, \ldots, K\}, \\ & \sum_{i \in S} \sum_{j \in S, j \neq i} x_{i j k} \leqslant|S|-1 \quad \forall k \in\{1, \ldots, K\}, \quad \forall S \subset X , 1<|S|< N, \\ & \sum_{k=1}^{K} \sum_{j \in \delta^{+}(i)} x_{i j k}=1 \quad \forall i \in\{1, \ldots, N\}, \\ & \sum_{i=1}^{N} q_{i} \sum_{j \in \delta^{+}(i)} x_{i j k} \leqslant C_{k} \quad \forall k \in\{1, \ldots, K\}, \\ & s_{i k}+d(i, j)-K\left(1-x_{i j k}\right) \leqslant s_{j k} \quad \forall(i, j) \in A, \quad \forall k \in\{1, \ldots, K\}, \\ & \quad \quad \quad a_{i} \leqslant s_{i k} \leqslant b_{i} \quad \forall i \in\{1, \ldots, N\}, \quad \forall k \in\{1, \ldots, K\}, \\ & \quad \quad \quad x_{ijk} \in \{0,1\} \quad \forall k \in \{1, \ldots, K\}, \quad \forall (i,j) \in A. \end{align} $$
목적함수(1)는 사용하는 arc의 거리 총합을 최소화하는 것이다. 제약식(2)-(4)는 차량 $k$의 flow를 나타내고 제약식(5)는 subtour를 제거해준다. 제약식(6)은 각 노드가 최대 한개의 차량에 의해 방문되어야함을 뜻하고 제약식(7)은 차량의 용량을 넘지않아야함을 뜻한다. 제약식(8)과 (9)는 time windows를 정의한다. 이 때 subtour 제약식의 수가 exponential이므로 Branch-and-Cut을 사용하여 dynamically 추가해준다.
Dantzig-Wolfe decomposition
위에서 정의한 MIP 모델에 Dantzig-Wolfe decomposition이 적용된다. 주어진 $k$에 대한 제약식(2)-(5)와 (7)에 해당하는 행렬 $B_k$를 고려한다. $B_k$로 정의된 polytope은 차량 $k$에 대한 valid path의 extreme points 집합 $\Omega_k$를 허용한다. 따라서 그 포인트 중 하나를 path들의 linear combination으로 쓸 수 있다. 이를 위해 극점 $\lambda^p_k$에 해당하는 path에 속하면 1 아니면 0인 계수 $x^p_{ijk}$를 사용한다. 따라서 $k \in \{1,\ldots,K\}$에 대해 솔루션 $x_{ijk}$를 다음과 같이 나타낼 수 있다.
$$ \begin{aligned} &x_{ijk} = \sum_{p \in \Omega_k} x^p_{ijk} \lambda^p_k \quad \forall (i,j) \in A, \\ &\sum_{p \in \Omega_k} \lambda^p_k = 1 \quad \forall k \in \{1,\ldots,K\}, \\ &\lambda^p_k \geqslant 0 \quad \forall p \in \Omega_k. \end{aligned} $$
차량 $k$에 대한 route $p$의 cost를 $c^p_k$로 정의힌다. 또한 양수인 정수 $a^p_{ik}$는 route $p$에 대해 차량 $k$가 노드 $i$를 방문한 횟수를 나타낸다.
$$ \begin{aligned} &c^p_k = \sum_{(i,j) \in A} c(i,j)x^p_{ijk} \quad \forall k \in \{1,\ldots,K\}, \quad \forall p \in \Omega_k, \\ &a^p_{ik} = \sum_{j \in \delta^+(i)} x^p_{ijk} \quad \forall i \in \{1,\ldots,\}N \quad \forall k \in \{1,\ldots,\}K, \quad \forall p \in \Omega_k, \end{aligned} $$
이러한 표현들을 원래 모델로 대체한다면 다음과 같은 decomposed model을 얻는다.
$$ \begin{aligned} \min \quad & \sum_{k=1}^{K} \sum_{p \in \Omega_k} c^p_k \lambda^p_k, \\ &\sum_{k=1}^{K} \sum_{p \in \Omega_k} a^p_{ik} \lambda^p_k = 1 \quad \forall i \in \{1,\ldots,N\}, \\ &\sum_{p \in \Omega_k} \lambda^p_k = 1 \quad \forall k \in \{1,\ldots,K\}, \\ &\lambda^p_k \geqslant 0 \quad \forall k \in \{1,\ldots,K\} \forall p \in \Omega_k. \end{aligned} $$
capacity, subtour elimination, time window 제약은 extreme point path의 validity를 정의하는 subproblems로 이동된다.
$$ \begin{aligned} \min \quad & \sum_{(i, j) \in A} d(i, j) x_{i j}, \\ & \sum_{j \in \delta^{+}(0)} x_{0 j }=1 , \\ & \sum_{i \in \delta^{-}(j)} x_{i j}-\sum_{i \in \delta^{+}(j)} x_{j i}=0 \quad \forall j \in\{1, \ldots, N\}, \\ & \sum_{i \in \delta^{-}(N+1)} x_{i, N+1}=1 , \\ & \sum_{i \in S} \sum_{j \in S, j \neq i} x_{i j} \leqslant|S|-1 \quad \forall S \subset X , 1<|S|< N, \\ & \sum_{i=1}^{N} q_{i} \sum_{j \in \delta^{+}(i)} x_{i j } \leqslant C_{k}, \\ & s_{i }+d(i, j)-K\left(1-x_{i j }\right) \leqslant s_{j } \quad \forall(i, j) \in A, \\ & \quad \quad \quad a_{i} \leqslant s_{i} \leqslant b_{i} \quad \forall i \in\{1, \ldots, N\}, \\ & \quad \quad \quad x_{ij} \in \{0,1\} \quad \forall (i,j) \in A. \end{aligned} $$ Identical vehicles
차량이 동일할 때 (총 용량이 같을 때) 모델의 일부를 다음과 같이 바꿀 수 있다. $$ \begin{aligned} \lambda^p = \sum^K_{k=1} \lambda^p_k \quad \forall p \in \Omega = \bigcup^K_{k=1} \Omega_k \end{aligned} $$ 그러면 다음과 같은 모델을 얻을 수 있다. $$ \begin{align} \min \quad & \sum_{p \in \Omega} c^p \lambda^p, \notag \\ &\sum_{p \in \Omega} a^p_{i} \lambda^p = 1 \quad \forall i \in \{1,\ldots,N\}, \\ &\sum_{p \in \Omega} \lambda^p = K, \notag \\ & \quad \quad \lambda^p \geqslant 0 \quad \forall p \in \Omega. \end{align} $$
decomposed model은 가능한 path 변수를 매우 많이 포함한다. 만약 $N$이 노드의 수라면 이론적으로 path 변수의 수는 $N$!개로 증가할 수 있다. 그렇기 때문에 column generation을 사용한다.
Branch-and-Price는 흔히 사용되는 branching 기법이다. column generation을 할 때 reduced cost를 확인하여 제한된 모델에 추가될 새로운 변수를 찾는데 이러한 과정을 pricing이라 한다. 더 이상 추가할 column이 없을 때까지 반복하며 변수가 fractional인 경우에는 branching을 해준다. 일반적으로 set partitioning 제약식(11)은 set covering 제약으로 바뀐다.
The pricing scheme
$\pi_i$와 $\pi_0$을 각각 제약식 (11)과 (12)에 대한 dual 이라고 한다면 reduced cost는 다음과 같다. $$ \begin{aligned} rc(p) = c(p) - \sum^N_{i=1} a^p_i \pi_i - \pi_0 = \sum_{(i,j) \in p} (d(i,j)-\pi_j) - \pi_0 \end{aligned} $$
따라서 subproblem은 다음과 같은 cost를 가지고 용량을 넘지 않는 the shortest elementary path를 찾는 문제가 된다. $$ \begin{aligned} &rc(i,j) = d(i,j)-\pi_j \quad \forall j \in \{1,\ldots,N\}, \\ &rc(i,N+1) = -\pi_0. \end{aligned} $$
Various possible subproblems
path $p = (i_0 = 0, i_1, \ldots, (N+1))$라 하자. resources는 $L$로 일반화 될 수 있고 $l$에 의해 인덱싱된다. $D^l_i$는 노드 $i$에서 resource $l$의 누적된 양을 나타낸다. 거리 함수 $d^l(i,j)$는 $i$와 $j$사이의 resource $l$의 누적을 정의한다. $[a^l_i,b^l_i]$는 resource와 노드 각각의 쌍으로 정의된다. 여기서는 두 개의 연속적인 노드 $i$와 $j$ 사이의 누적된 resource의 증가는 triangle inequality를 만족해야한다는 것을 이용한다. $$ \begin{aligned} d^l(i,k) \leqslant d^l(i,j) + d^l(j,k) \quad \forall l = 1\ldots L. \end{aligned} $$
Theorem 1. triangle inequality에 대한 resource 누적과 노드 사이의 cost 누적이 strictly positive일 때, non-elementary path를 가지는 마스터 문제의 optimal integer solution은 elementary path만을 포함한다.
일반적으로 최단경로 서브문제는 cycle이 허용되는 pseudo-polynomial labeling algorithm으로 풀린다. 그러나 elementary path만 사용된다면 relaxed 마스터 문제는 더 제한되고 더 좋은 bound가 제공될 것이다.
Labeling algorithm
노드 $i$에서 partial path $p$는 label $E_p = (rc_p, D^0_p, \ldots , D^L_p)$와 관련되어 있다. 레이블링 알고리즘에서 사용되는 기본적인 rule은 dominance rule이고 다음을 만족하면 partial path $p_1$은 다른 partial path $p_2$를 dominate한다. $$ \begin{align} &rc_1 \leqslant rc_2, \\ &D^l_1 \leqslant D^l_2 \quad \forall l \in \{0,\ldots L\} \end{align} $$ dominance rule은 elementary shortes path에 직접적으로 사용될 수 없다. 따라서 이 논문의 중점은 실질적이고 효율적인 알고리즘의 수정을 제안하는 것이다.
이 논문에서는 Ryan-Foster rules에 기초한 branching 기법을 사용한다. 같은 node $i$와 $j$를 공유하는 두 개의 fractional routes를 찾는다. (한 경로는 arc $(i,j)$를 사용하고 다른 경로는 사용하지 않는다.) 각 branch에서 최단 경로 서브문제는 문제의 구조를 깨지 않고 쉽게 수정될 수 있다.
좋지 않은 lower bound를 가지는 노드를 prune하기 위해 bound의 quality가 중요한데 이 논문에서는 relaxation의 quality를 향상하기 위한 두 가지 방법을 제시한다. 첫 번째는 relaxation에 cutting plane을 추가하는 것이고 두 번째는 elementary shortest path subproblem에 기초한 것이다. SPRCTW를 사용할 경우 마스터 문제를 MP로 표시하고 ESPRCTW를 사용할 경우 EMP로 표시한다. MP에서 통합 제약을 제거하면 RMP로 표시하고 EMP에서 제거하면 REMP로 표시한다.
Simple example
depot에서 매우 먼 두 개의 노드 $i$와 $j$를 가지는 문제에 대해 다음과 같이 가정한다. $$ \begin{aligned} &d(0,i) = d(0,j) = 100,\\ &d(i,j) == 1. \end{aligned} $$ 용량과 time window는 크다고 가정한다. EMP의 optimal relaxed solution은 $LB_{elem}$ = 201 이 되도록 unique route 0-$i$-$j$-$(N+1)$로 만들어 진다. cycles가 허용되면 0-$(i-j)^n$-($N$+1)의 route 형식으로 $i$-$j$가 $n$번 반복된다.
relaxed problem으로 부터 얻은 솔루션을 향상시키는 가장 흔한 방법은 $k$-path cuts과 같은 cutting plane을 추가하는 것이다. $S$를 노드 집합, $\delta(S)$를 $S$에서의 outgoing arcs의 집합 ($\delta(S)$ = {($i$,$j$ $\in$ $A$/ $i$ $\in$ $S$, $j$ $\notin$ $S$}), $\mu^p_S$를 path $p$가 $\delta(S)$에서 가지는 arcs의 수라고 하자. 어떤 $k$ $\leqslant$ $\kappa(S)$에 대해 그 집합에서 최소 한개의 노드를 포함하는 경로에 해당하는 변수 $\lambda$에 $k$-path cut으로 알려진 새로운 제약을 다음과 같이 추가할 수 있다. $$ \begin{aligned} \sum_{p \in \Omega} \mu^p_S \lambda^p \geqslant k. \end{aligned} $$ cut을 추가하는 것은 lower bound를 향상 시킬 수 있다. 그러나 MP에 subtour cut을 추가하여 얻은 bound는 EMP에서 얻은 bound와 같지 않다. 예를 들어 세 개의 노드 $i$, $j$, $k$를 가지고 있다고 가정하면 경로의 집합은 각각 $ \frac{1}{2}$의 값을 가질 수 있다.
0-$j$-$k$-($N$+1),
0-$i$-$j$-$k$-$i$-($N$+1).
이 솔루션이 어떤 subtour cut을 위반하지 않더라도 cycle을 포함하여 EMP의 솔루션이 될 수 없을 것이다. ESP가 풀기 더 어렵지만 cutting plane을 사용할 때 relaxation에 추가되는 violated cut을 분리하기 위해 다른 복잡한 알고리즘을 사용해야만 한다.
Use of elementary paths
MP와 EMP의 제약조건이 동일하고 column 집합이 다른 하나에 포함되어 있으면 MP는 EMP의 relaxation이고 RMP는 REMP의 relaxation이다. 따라서 서브문제에 ESPRCTW를 사용한다. 알고리즘의 worst practical efficiency와 better quality of bounds 사이에서 적절한 타협점을 갖도록 한다.
elementary path 문제에 대한 labeling algorithm의 수정에 대해 제안하는데 두 개의 주요한 차이점이 적용된다.
- partial route는 부분 경로에서 이미 존재하는 노드로 갈 수 없다.
- label은 dominance rule을 사용하여 직접적으로 파악할 수 없다.
A preliminary modified dominance rule
수정된 지배 규칙은 부분 경로 $p_1$이 다른 부분 경로 $p_2$를 지배하는 충분 조건이 (13)과 (14) 조건을 만족하고 노드 집합 $V(p_2)$에 $V(p_1)$을 포함할 때 사용된다. $$ \begin{align} V(p_1) \subseteq V(p_2). \end{align} $$ 기본적인 새로운 지배 규칙은 많은 레이블을 만들어낼 것이다. 실제로 노드의 집합이 다른 것에 포함되지 않는((15)를 만족하지 않는) 두 개의 부분 경로는 지배 규칙에 해당되지 않는다. 따라서 이 규칙에 대한 complete 수정과 heuristic 수정에 대한 개선을 소개한다.
Exact improvement of the dominance rule
$p_1$의 일부 노드를 거치면서 얻을 수 있는 reduced cost의 예상되는 개선을 추정함으로써 지배 규칙을 향상시킬 수 있다. $p_1$과 $p_2$를 같은 노드 $m$에서 끝나는 두 개의 부분 경로라고 하자. $V(p)$는 부분 경로 $p$에 의해 방문된 노드의 집합이다. $V(p_1)$ \ $V(p_2)$ = {n}일 때 근사치를 고려해보자.
1. Bound on improvement with $\pi_n$ : $p^*_2$가 부분 경로 $p_2$의 확장이기 때문에 $n$을 제외하고 $p^*_1$을 같은 방법으로 만들 수 있다. $p^*_2$에서 이전 노드 $i$와 다음 노드 $j$를 사용하여 다음과 같이 나타낼 수 있다. $$ \begin{aligned} rc^*_2 - rc^*_1 = c(i,n) + c(n,j) - c(i,j) - \pi_n + rc_2 -rc_1. \end{aligned} $$ 따라서 다음과 같은 경우에만 $p^*_2$가 $p^*_1$보다 더 좋다. $$ \begin{aligned} c(i,n) + c(n,j) - c(i,j) - \pi_n + rc_2 -rc_1 < 0. \end{aligned} $$ 비용 부분(triangle inequality로 인해 항상 양수이다)을 과소평가함으로써 $p_2$를 제거하기 위한 충분 조건은 다음과 같다. $$ \begin{align} - \pi_n \geqslant rc_1 -rc_2. \end{align} $$ 2. Bounds on improvement with $\pi_n$ − $minAddedArcCost_n$: 비용 부분의 더 나은 근사를 사용하고 다음과 같은 식을 사용하여 과소평가 한다. $$ \begin{align} minAddedArcCost_n = min_{i\in prec(n),j\in succ(n)}(c(i, n) + c(n, j) − c(i, j)), \end{align} $$ $prec(n)$은 노드 $n$의 가능한 predecessors의 집합, $succ(n)$은 가능한 successors의 집합이다. 이는 각 노드 $n$에 대한 알고리즘 초기화 단계에서 계산될 수 있다. 따라서 충분 조건은 다음과 같다. $$ \begin{align} minAddedArcCost_n - \pi_n \geqslant rc_1 - rc_2. \end{align} $$ (16)과 (17) 두 개의 조건은 더 많은 레이블을 파악하는데 사용될 수 있다. 이러한 조건들은 $Card(V(p_1)$\ $V(p_2))$ > 1인 경우에 일반화 될 수 있다. 그러나 좋은 bound를 찾는 것이 어렵기 때문에 알고리즘을 $Card(V(p_1)$\ $V(p_2))$ $\leqslant$ 2인 경우로 제한했다.
Computational Results
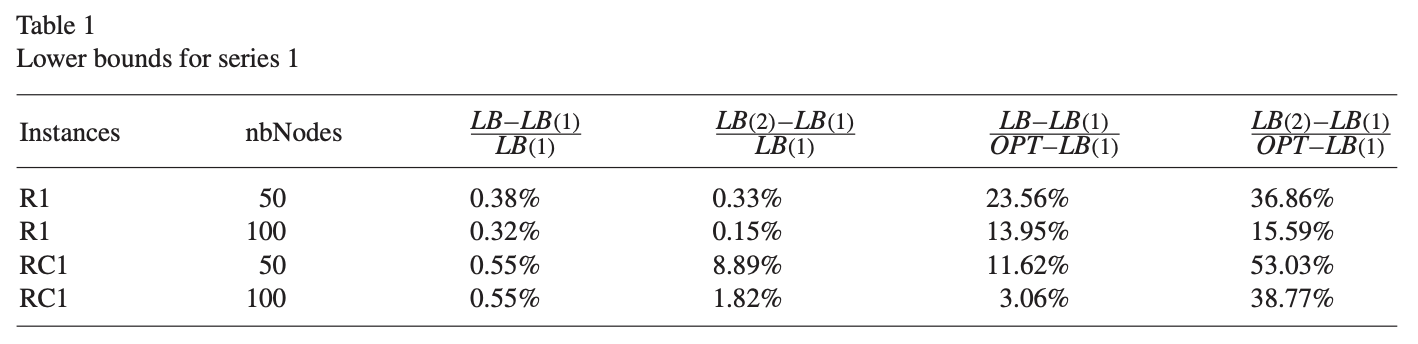
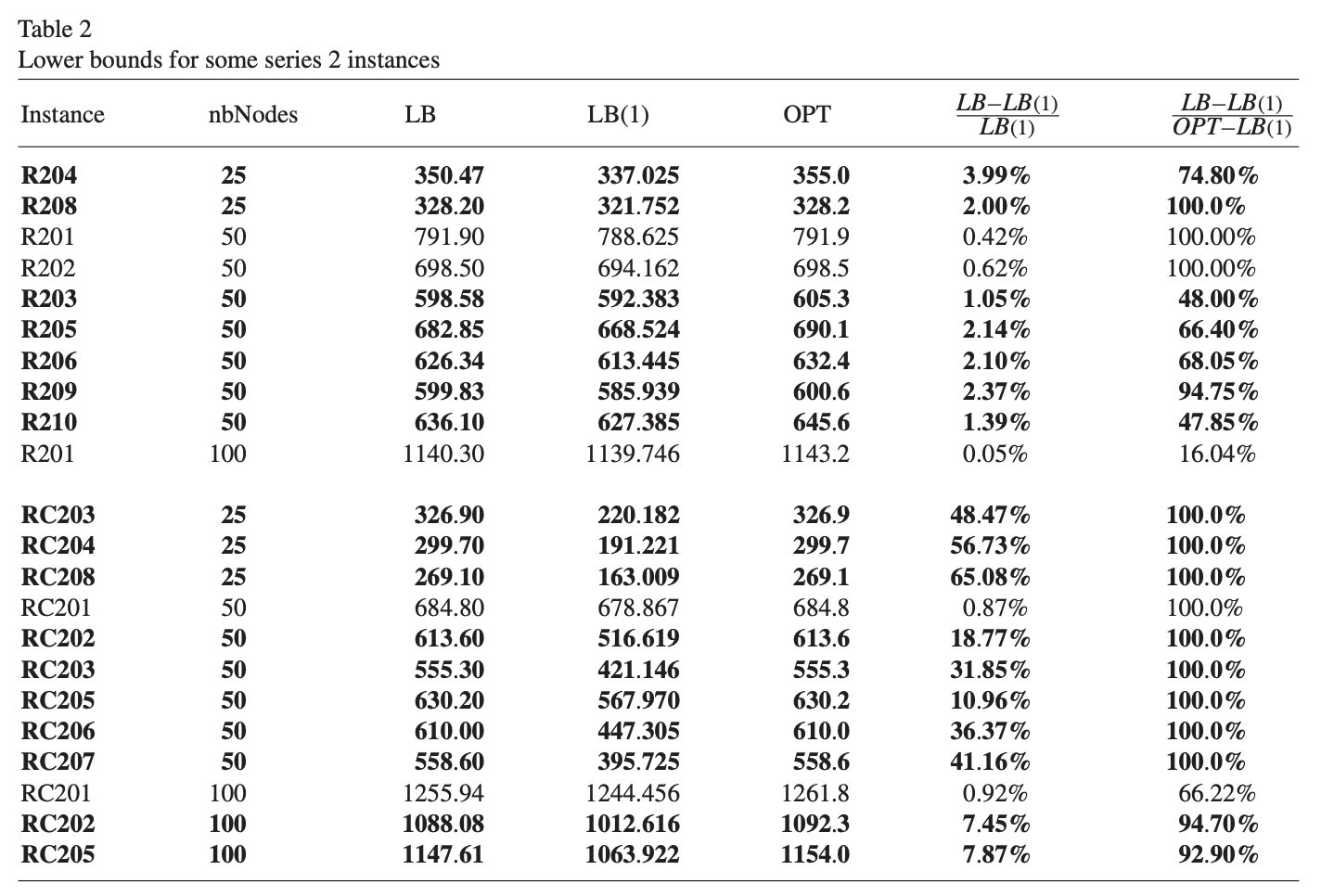
데이터는 Solomon을 사용한다. Table 1에서는 R1과 RC1에서 얻은 bound를 [11]과 비교한다.
- $i$-$j$-$i$ 형태의 cycle만 금지하는 서브문제에 해당하는 $LB$와 [11]의 $LB(1)$ 비교
- Branch-and-Price root node에 subtour cut과 2-path cut을 추가한 $LB(2)$와 [11]의 $LB(1)$ 비교
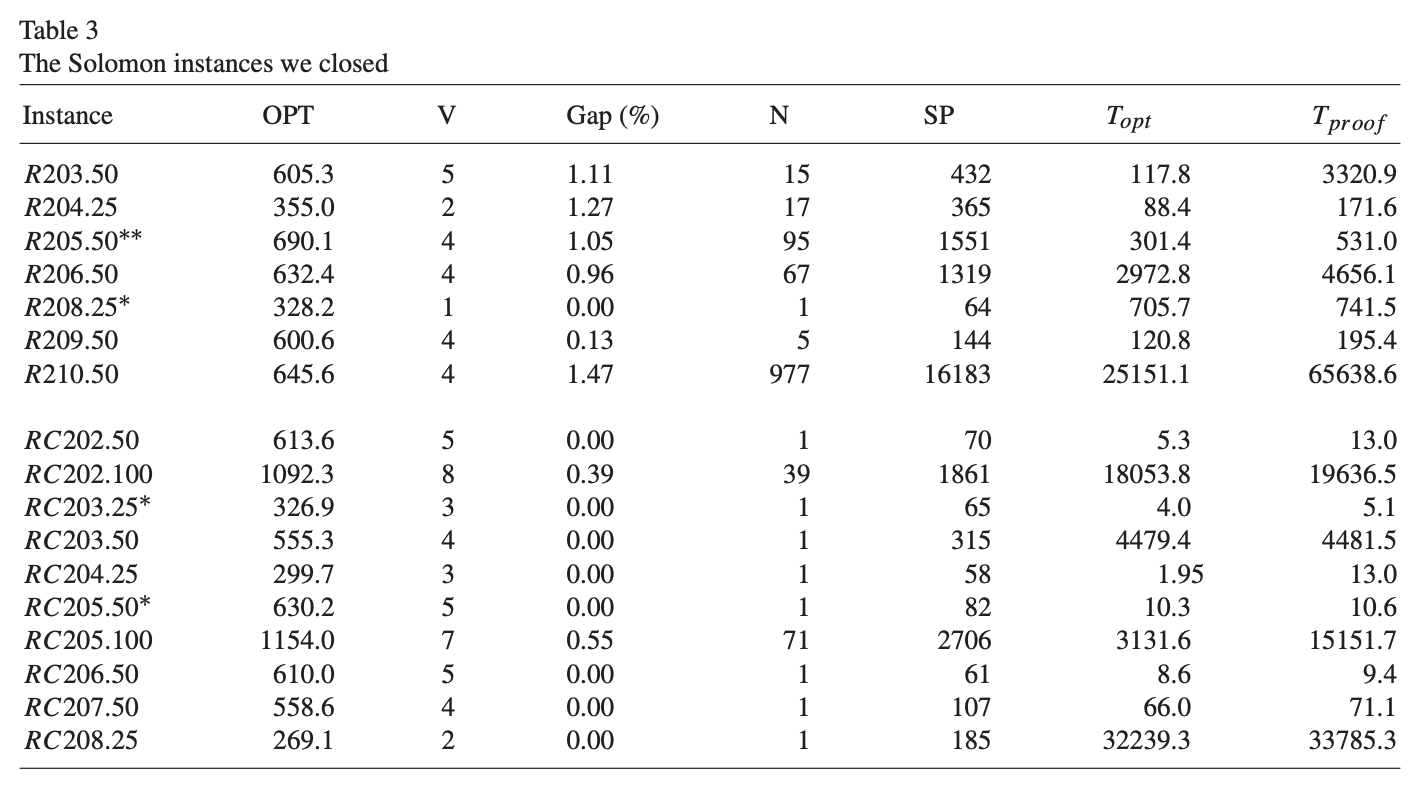
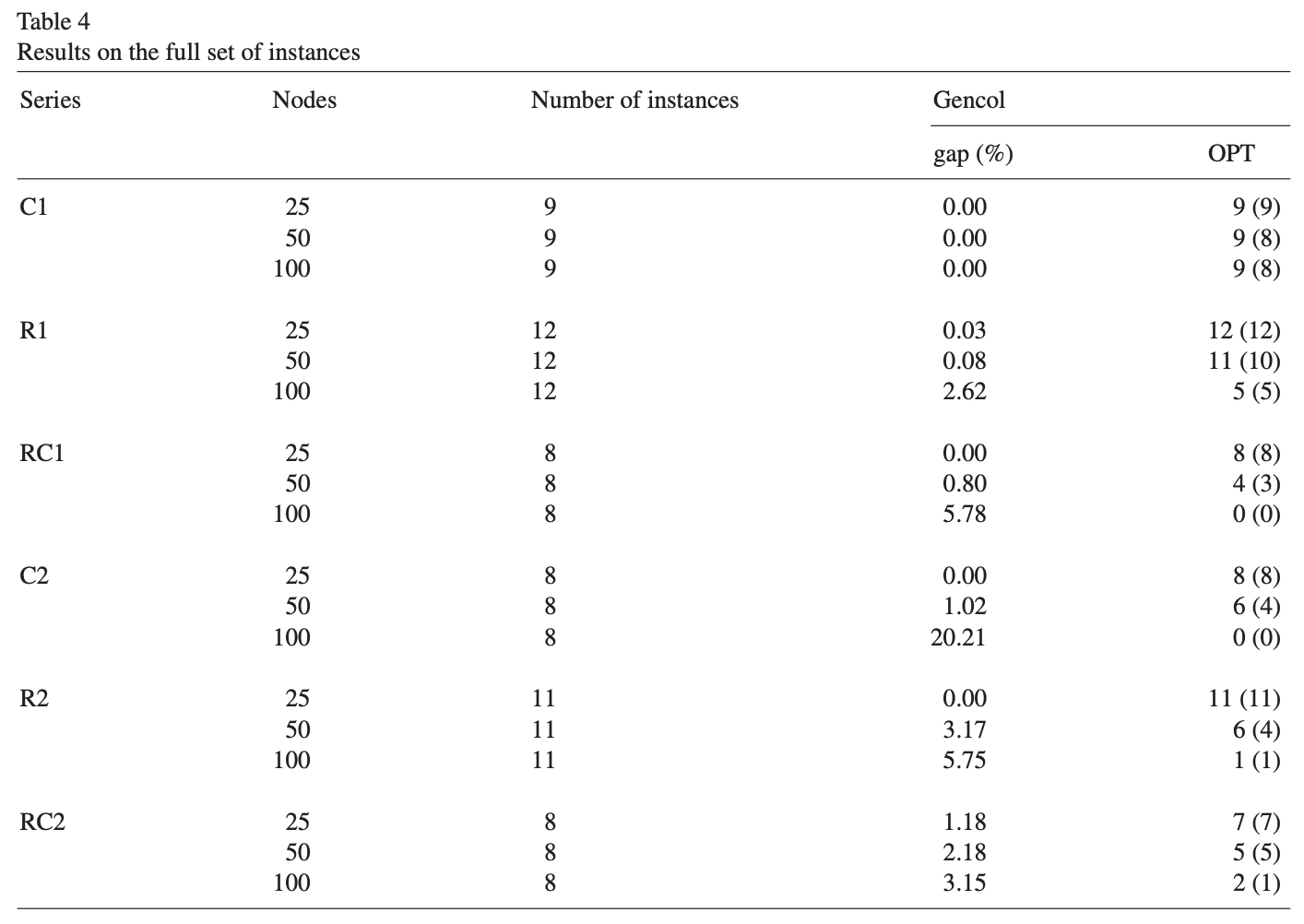
논문의 결론은 다음과 같이 정리할 수 있다.
- 일반적인 elementary shortest path 알고리즘에 대한 개선을 제안한다.
- elementary shortest path가 수정된 알고리즘이 사용될 때 실질적으로 유용함을 보여준다.
- 새로운 최적해를 찾기 위해 cutting planes를 사용하는 것은 lower bound를 향상시키는 또다른 방법이다.
Cite
Chabrier, A. (2006). Vehicle routing problem with elementary shortest path based column generation. Computers & Operations Research, 33(10), 2972-2990. 논문 링크