발현 (Emergence)
Emergence는 ABM의 가장 중요하고 독특한 특징으로, 복잡하고 예상치 못한 시스템 다이나믹스가 기본적인 프로세스를 모델링하는 방법에서 나온다는 것이다. 여기서 예상치 못한다는 뜻은 단순히 생각만으로 예측하기 어렵거나 불가능함을 뜻한다. Emergence는 단순히 모델 객체의 성질이 합쳐진 것도, 각각의 성질로부터 쉽게 예측될 수 있는 것도 아니다.
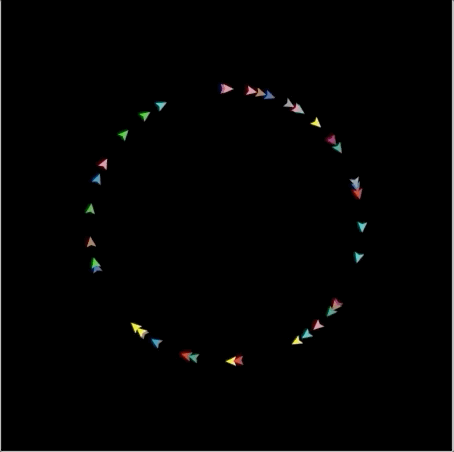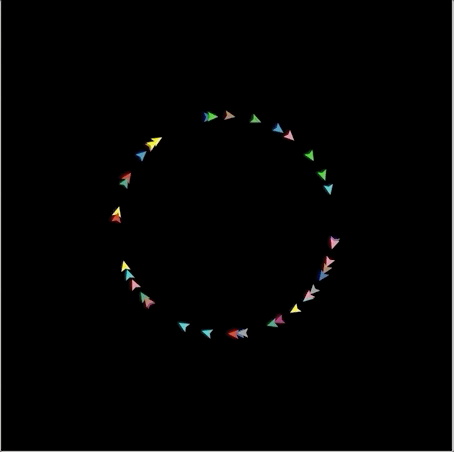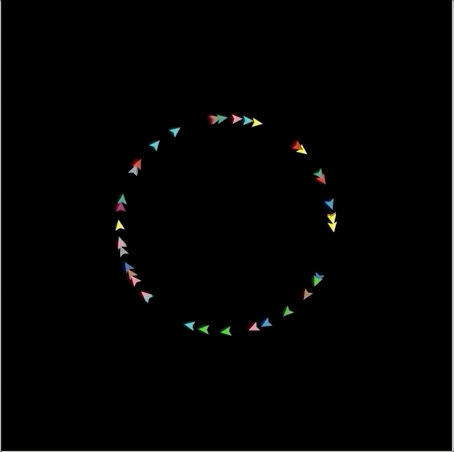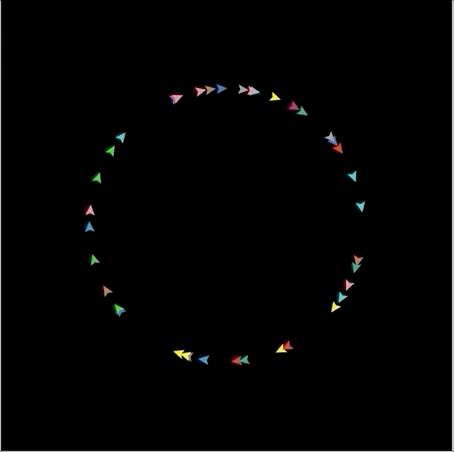

관련된 간단한 문제를 만들어보자. 40개의 turtle을 만들고 'speed' attribute를 추가한다. turtle들을 앞으로 10만큼 이동시키고 오른쪽으로 90도 돌리면 어떤 모양이 될까? 놀랍게도 왼쪽 그림과 같이 원 모양이 만들어진다. 이를 turtle의 속도만큼 앞으로 이동하고 오른쪽으로 1만큼 계속 돌리면 오른쪽 그림과 같이 원이 커졌다가 줄어드는 현상을 볼 수 있다.
또 다른 예시로 Simple Birth Rates Model을 들 수 있다. 이 모델은 두 개의 종 (빨간색 turtle, 파란색 turtle) 사이의 출생률 차이가 각 모집단의 객체수에 어떤 영향을 미치는지 시뮬레이션하기 위해 설계되었다. 두 종은 time step 마다 생산하는 자손의 수에만 차이가 있고 죽을 확률은 같다. 두 종의 상대적인 출생률에 따라 한 종이 멸종할 때까지 얼마나 시간이 걸리는지 알아본다. 이 모델에서 fertility를 조절하여 출생률을 바꿀 수 있으며, 예를 들어 fertility 3.4라면 최소 3명의 자손을 낳고 40%의 확률로 4번째 자손을 낳을 수 있다는 뜻이다. 두 종의 출생률이 비슷하면 어느 한 종이 멸종하기까지 오랜 시간이 걸리고 출생율의 차이가 커질수록 출생율이 작은 종이 더 빨리 멸종하는 것을 확인할 수 있다.
민감도 분석 (Sensitivity Experiments)
민감도 분석은 시뮬레이션에서 특정한 파라미터나 input에 따라 모델이 어떻게 변하는지 분석하는 것이다. 이 때, 모델은 확률적인(stochastic) 특성을 가지기 때문에 같은 파라미터로 시뮬레이션해도 완전히 똑같은 결과가 나오지 않는다. 따라서 각각의 시나리오에 대해 최소 30번 이상 실행하여 평균값을 얻어야 한다. NetLogo에서는 Tools > BehaviorSpace 탭으로 들어가면 여러 조건을 주고 실험할 수 있으며 결과를 엑셀 등으로 저장할 수 있다.
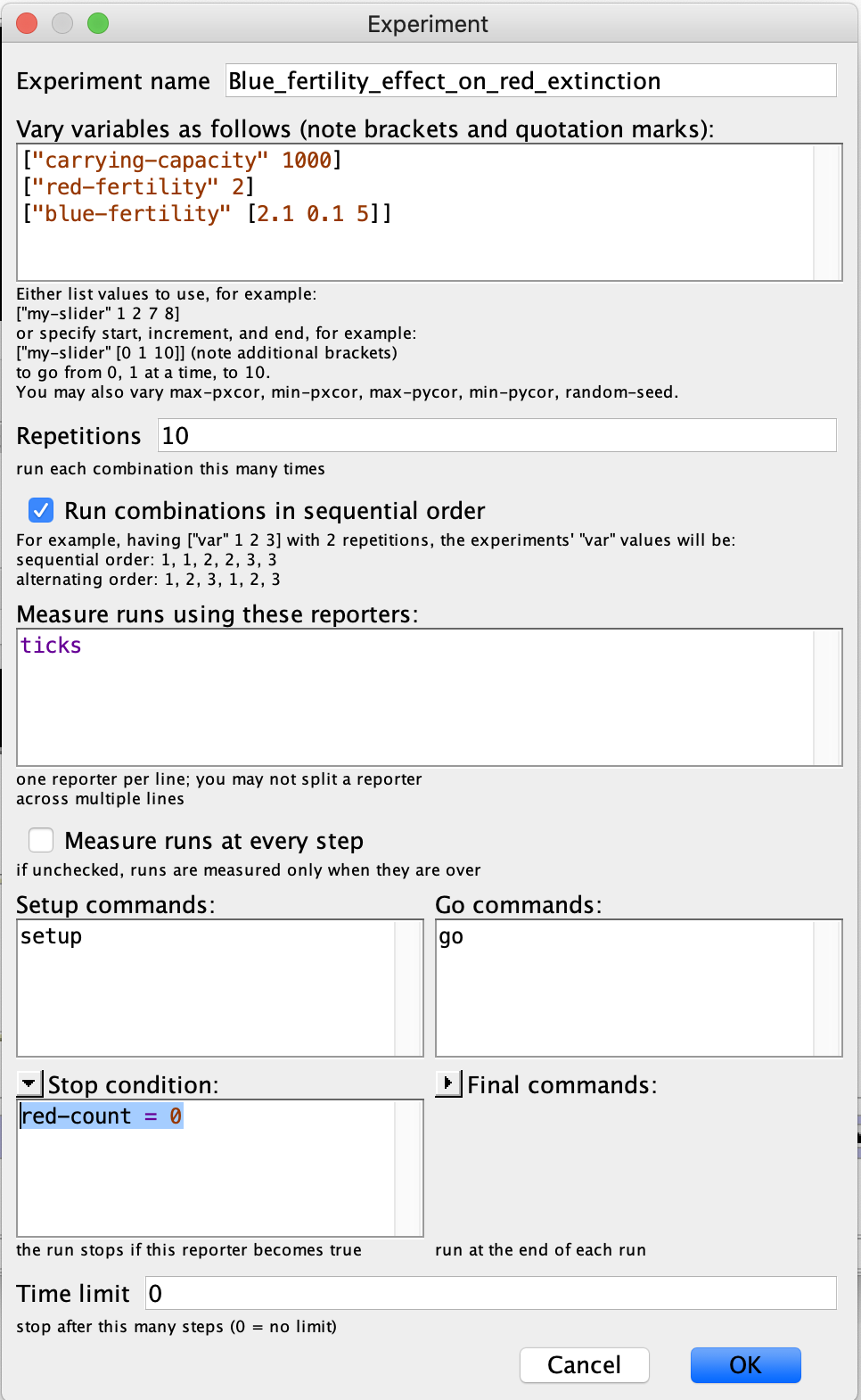
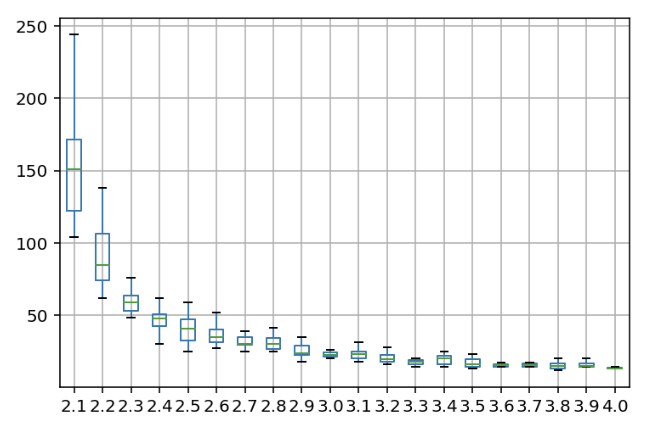
실험결과를 이용해 오른쪽 그림과 같이 boxplot을 그려 분석해볼 수 있다. 빨간색 turtle의 출생률은 2로 고정시키고 파란색 turtle의 출생률을 증가시켰을 때, 빨간색 turtle이 멸종하는 시간이 점점 더 짧아짐을 볼 수 있다.
앞서 살펴본 Flocking 모델에서도 Emergent behavior를 관찰할 수 있다. 그러나 완전히 발현되기까지 warm-up 단계(대략 400ticks 부터 발현)를 거칠 수도 있다. Emergence를 구체화하기 위해서는 정량적인 방법 (quantitative measurements)이 필요하며, 예를 들어 flockmates의 수나 거리를 평균적으로 구해보거나 방향에 대한 표준편차 등을 구해보는 것 등이 있다. 또는 대조적인 시나리오를 비교해보는 방법도 있다. Flocking 모델을 예로 들면, flockmate를 범위 안에 있는 모든 turtle로 정의할지, 가장 가까운 turtle만 정의할지에 따라 결과가 달라진다.
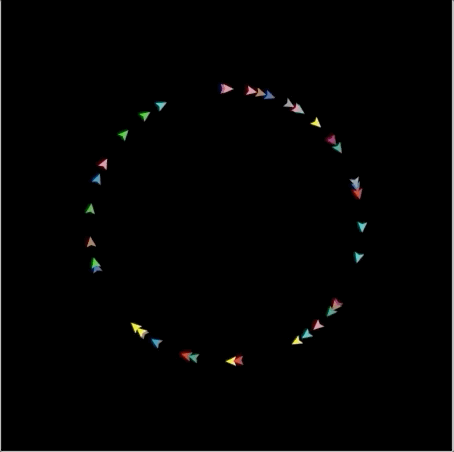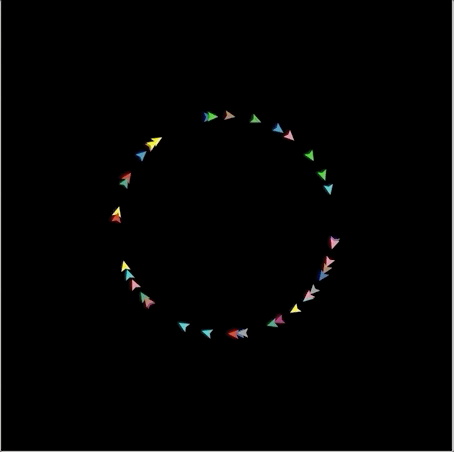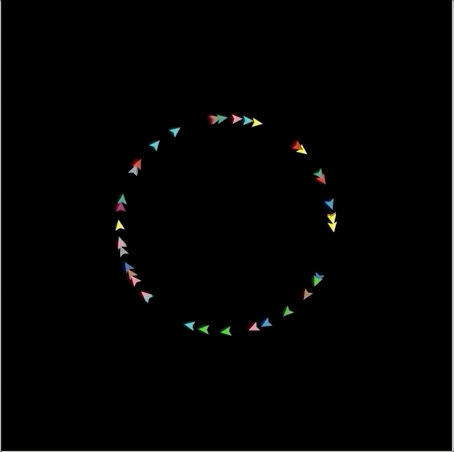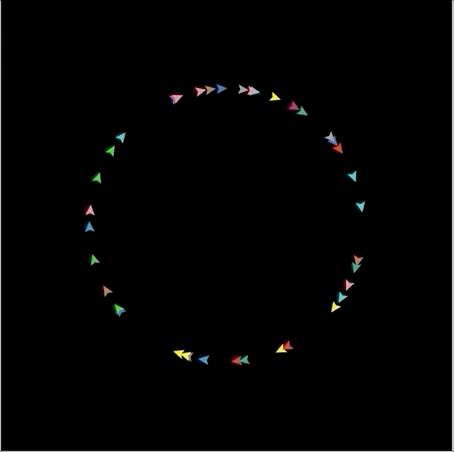

관련된 간단한 문제를 만들어보자. 40개의 turtle을 만들고 'speed' attribute를 추가한다. turtle들을 앞으로 10만큼 이동시키고 오른쪽으로 90도 돌리면 어떤 모양이 될까? 놀랍게도 왼쪽 그림과 같이 원 모양이 만들어진다. 이를 turtle의 속도만큼 앞으로 이동하고 오른쪽으로 1만큼 계속 돌리면 오른쪽 그림과 같이 원이 커졌다가 줄어드는 현상을 볼 수 있다.
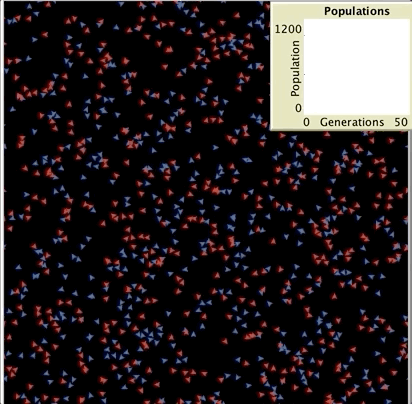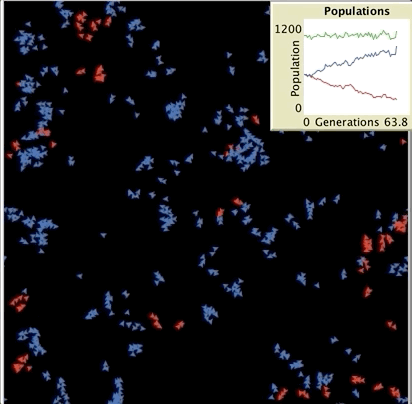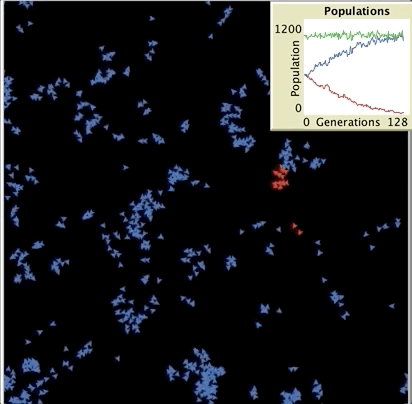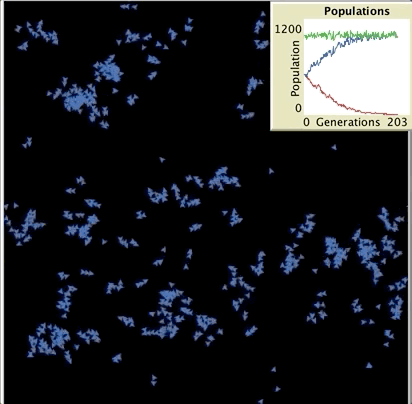
또 다른 예시로 Simple Birth Rates Model을 들 수 있다. 이 모델은 두 개의 종 (빨간색 turtle, 파란색 turtle) 사이의 출생률 차이가 각 모집단의 객체수에 어떤 영향을 미치는지 시뮬레이션하기 위해 설계되었다. 두 종은 time step 마다 생산하는 자손의 수에만 차이가 있고 죽을 확률은 같다. 두 종의 상대적인 출생률에 따라 한 종이 멸종할 때까지 얼마나 시간이 걸리는지 알아본다. 이 모델에서 fertility를 조절하여 출생률을 바꿀 수 있으며, 예를 들어 fertility 3.4라면 최소 3명의 자손을 낳고 40%의 확률로 4번째 자손을 낳을 수 있다는 뜻이다. 두 종의 출생률이 비슷하면 어느 한 종이 멸종하기까지 오랜 시간이 걸리고 출생율의 차이가 커질수록 출생율이 작은 종이 더 빨리 멸종하는 것을 확인할 수 있다.
민감도 분석 (Sensitivity Experiments)
민감도 분석은 시뮬레이션에서 특정한 파라미터나 input에 따라 모델이 어떻게 변하는지 분석하는 것이다. 이 때, 모델은 확률적인(stochastic) 특성을 가지기 때문에 같은 파라미터로 시뮬레이션해도 완전히 똑같은 결과가 나오지 않는다. 따라서 각각의 시나리오에 대해 최소 30번 이상 실행하여 평균값을 얻어야 한다. NetLogo에서는 Tools > BehaviorSpace 탭으로 들어가면 여러 조건을 주고 실험할 수 있으며 결과를 엑셀 등으로 저장할 수 있다.


실험결과를 이용해 오른쪽 그림과 같이 boxplot을 그려 분석해볼 수 있다. 빨간색 turtle의 출생률은 2로 고정시키고 파란색 turtle의 출생률을 증가시켰을 때, 빨간색 turtle이 멸종하는 시간이 점점 더 짧아짐을 볼 수 있다.
앞서 살펴본 Flocking 모델에서도 Emergent behavior를 관찰할 수 있다. 그러나 완전히 발현되기까지 warm-up 단계(대략 400ticks 부터 발현)를 거칠 수도 있다. Emergence를 구체화하기 위해서는 정량적인 방법 (quantitative measurements)이 필요하며, 예를 들어 flockmates의 수나 거리를 평균적으로 구해보거나 방향에 대한 표준편차 등을 구해보는 것 등이 있다. 또는 대조적인 시나리오를 비교해보는 방법도 있다. Flocking 모델을 예로 들면, flockmate를 범위 안에 있는 모든 turtle로 정의할지, 가장 가까운 turtle만 정의할지에 따라 결과가 달라진다.