Stochastic Gradient Descent
Stochastic Gradient Descent(SGD)와 그 변형들은 머신러닝과 특히 딥러닝에서 가장 많이 사용된 최적화 알고리즘이다.
learning rate는 시행착오(trial and error)를 통해 선택될 수 있지만 주로 시간의 함수로써 목적함수의 plot인 학습 곡선(curves)을 모니터링함으로써 선택하는 것이 가장 좋다. 선형 스케쥴을 사용할 때, 선택할 파라미터는 $\epsilon_{0}, \epsilon_{\tau}, \tau$ 이다. 일반적으로 $\tau$는 트레이닝 셋을 통해 수백번 통과하는데 필요한 반복 횟수로 설정되고 $\epsilon_{\tau}$는 $\epsilon_{0}$의 약 1%로 설정해야 한다.
그렇다면 $\epsilon_{0}$(초기 learning rate)은 어떻게 설정해야할까? 값이 너무 크면 학습 곡선이 격렬한(violent) 움직임(oscillations)을 보이고 비용 함수는 상당히 증가할 것이다. 반면 learning rate가 너무 낮으면 학습이 느리게 진행되고 초기 learning rate가 너무 낮으면 학습이 높은 비용값에 머무른다. 일반적으로 최적의 초기 learning rate는 처음 100번 정도 반복 후 가장 좋은 값을 내는 learning rate 보다는 높다. 그러므로 처음 몇 번의 반복을 모니터링하여 가장 좋은 learning rate보다 높은 값을 사용하지만 너무 높은 값은 심한 불안정을 초래하므로 적당한 값을 사용해야한다.
SGD와 관련된 미니배치 또는 online gradient-based optimization의 가장 중요한 특성은 업데이트당 계산 시간이 트레이닝 예제 수에 따라 증가하지 않는다는 것이다. 이는 심지어 트레이닝 예제의 수가 매우 커져도 수렴할 수 있음을 시사한다. 충분히 큰 데이터셋의 경우, SGD는 전체 트레이닝 셋을 처리하기 전에 마지막 테스트셋 에러의 일정한 허용오차(tolerance)이내로 수렴할 것이다.
SGD가 convex 문제에 적용될 때, 초과(excess) 에러는 $k$번 반복 후 $O(1/\sqrt{k})$ 이고, strongly convex인 경우 $O(1/k)$이다. Batch gradient descent는 이론상 SGD보다 수렴률이 더 높다. 그러나 $\text { Cramér-Rao }$는 일반화 에러가 $O(1/k)$보다 빨리 감소할 수 없다고 주장하고 있다. 큰 데이터셋을 가지는 SGD는 매우 적은 예제에 대해 기울기를 평가하면서 빠르게 초기 진행이 이루어지는 능력은 그것의 slow 수렴근사보다 더 크다. 학습과정동안 미니배치 사이즈를 점점 증가시킴으로써 배치와 SGD의 이점을 trade off 할 수 있다.
Momentum
SGD가 유명한 최적화 방법으로 남아있지만 이를 통한 학습은 간혹 느리게 진행될 수 있다. momentum 방법(Polyak,1964)은 특히 높은 곡률(curvature), 작지만 일정한 기울기 또는 noisy 기울기를 갖는 학습을 가속화하기 위해 설계되었다. 모멘텀 알고리즘은 이전 기울기들이 기하급수적으로 감소하는 이동 평균을 누적하여 그 방향으로 계속 움직인다.
Nesterov Momentum
Sutskever et al.(2013)은 모멘텀 알고리즘의 변형을 다음과 같이 제안했다. $$ \begin{array}{l}\boldsymbol{v} \leftarrow \alpha \boldsymbol{v}-\epsilon \nabla_{\boldsymbol{\theta}}\left[\frac{1}{m} \sum_{i=1}^{m} L\left(\boldsymbol{f}\left(\boldsymbol{x}^{(i)} ; \boldsymbol{\theta}+\alpha \boldsymbol{v}\right), \boldsymbol{y}^{(i)}\right)\right] \\ \boldsymbol{\theta} \leftarrow \boldsymbol{\theta}+\boldsymbol{v}\end{array} $$ Nesterov 모멘텀과 표준 모멘텀의 차이는 어디서 기울기가 평가되는가 이다. Nesterov 모멘텀은 현재 속도가 적용된 후에 기울기가 평가된다. 따라서 Nesterov 모멘텀은 표준 모멘텀 방법에 보정(correction) 요소를 추가하려는 것으로 해석할 수 있다. convex batch gradient의 경우 Nesterov 모멘텀은 초과 에러의 수렴율을 $O(1/k)$ 에서 $O(1/k^2)$로 가져온다. 안타깝게도 SGD에서 Nesterov 모멘텀은 수렴율을 향상시키지 않는다.
Stochastic Gradient Descent(SGD)와 그 변형들은 머신러닝과 특히 딥러닝에서 가장 많이 사용된 최적화 알고리즘이다.

learning rate는 시행착오(trial and error)를 통해 선택될 수 있지만 주로 시간의 함수로써 목적함수의 plot인 학습 곡선(curves)을 모니터링함으로써 선택하는 것이 가장 좋다. 선형 스케쥴을 사용할 때, 선택할 파라미터는 $\epsilon_{0}, \epsilon_{\tau}, \tau$ 이다. 일반적으로 $\tau$는 트레이닝 셋을 통해 수백번 통과하는데 필요한 반복 횟수로 설정되고 $\epsilon_{\tau}$는 $\epsilon_{0}$의 약 1%로 설정해야 한다.
그렇다면 $\epsilon_{0}$(초기 learning rate)은 어떻게 설정해야할까? 값이 너무 크면 학습 곡선이 격렬한(violent) 움직임(oscillations)을 보이고 비용 함수는 상당히 증가할 것이다. 반면 learning rate가 너무 낮으면 학습이 느리게 진행되고 초기 learning rate가 너무 낮으면 학습이 높은 비용값에 머무른다. 일반적으로 최적의 초기 learning rate는 처음 100번 정도 반복 후 가장 좋은 값을 내는 learning rate 보다는 높다. 그러므로 처음 몇 번의 반복을 모니터링하여 가장 좋은 learning rate보다 높은 값을 사용하지만 너무 높은 값은 심한 불안정을 초래하므로 적당한 값을 사용해야한다.
SGD와 관련된 미니배치 또는 online gradient-based optimization의 가장 중요한 특성은 업데이트당 계산 시간이 트레이닝 예제 수에 따라 증가하지 않는다는 것이다. 이는 심지어 트레이닝 예제의 수가 매우 커져도 수렴할 수 있음을 시사한다. 충분히 큰 데이터셋의 경우, SGD는 전체 트레이닝 셋을 처리하기 전에 마지막 테스트셋 에러의 일정한 허용오차(tolerance)이내로 수렴할 것이다.
SGD가 convex 문제에 적용될 때, 초과(excess) 에러는 $k$번 반복 후 $O(1/\sqrt{k})$ 이고, strongly convex인 경우 $O(1/k)$이다. Batch gradient descent는 이론상 SGD보다 수렴률이 더 높다. 그러나 $\text { Cramér-Rao }$는 일반화 에러가 $O(1/k)$보다 빨리 감소할 수 없다고 주장하고 있다. 큰 데이터셋을 가지는 SGD는 매우 적은 예제에 대해 기울기를 평가하면서 빠르게 초기 진행이 이루어지는 능력은 그것의 slow 수렴근사보다 더 크다. 학습과정동안 미니배치 사이즈를 점점 증가시킴으로써 배치와 SGD의 이점을 trade off 할 수 있다.
Momentum
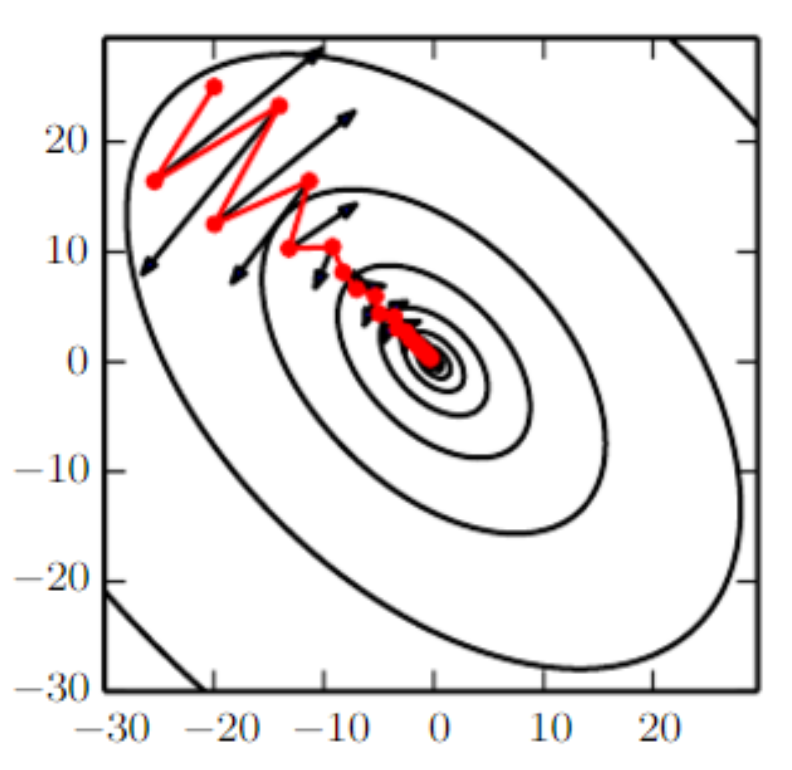
SGD가 유명한 최적화 방법으로 남아있지만 이를 통한 학습은 간혹 느리게 진행될 수 있다. momentum 방법(Polyak,1964)은 특히 높은 곡률(curvature), 작지만 일정한 기울기 또는 noisy 기울기를 갖는 학습을 가속화하기 위해 설계되었다. 모멘텀 알고리즘은 이전 기울기들이 기하급수적으로 감소하는 이동 평균을 누적하여 그 방향으로 계속 움직인다.
Nesterov Momentum
Sutskever et al.(2013)은 모멘텀 알고리즘의 변형을 다음과 같이 제안했다. $$ \begin{array}{l}\boldsymbol{v} \leftarrow \alpha \boldsymbol{v}-\epsilon \nabla_{\boldsymbol{\theta}}\left[\frac{1}{m} \sum_{i=1}^{m} L\left(\boldsymbol{f}\left(\boldsymbol{x}^{(i)} ; \boldsymbol{\theta}+\alpha \boldsymbol{v}\right), \boldsymbol{y}^{(i)}\right)\right] \\ \boldsymbol{\theta} \leftarrow \boldsymbol{\theta}+\boldsymbol{v}\end{array} $$ Nesterov 모멘텀과 표준 모멘텀의 차이는 어디서 기울기가 평가되는가 이다. Nesterov 모멘텀은 현재 속도가 적용된 후에 기울기가 평가된다. 따라서 Nesterov 모멘텀은 표준 모멘텀 방법에 보정(correction) 요소를 추가하려는 것으로 해석할 수 있다. convex batch gradient의 경우 Nesterov 모멘텀은 초과 에러의 수렴율을 $O(1/k)$ 에서 $O(1/k^2)$로 가져온다. 안타깝게도 SGD에서 Nesterov 모멘텀은 수렴율을 향상시키지 않는다.