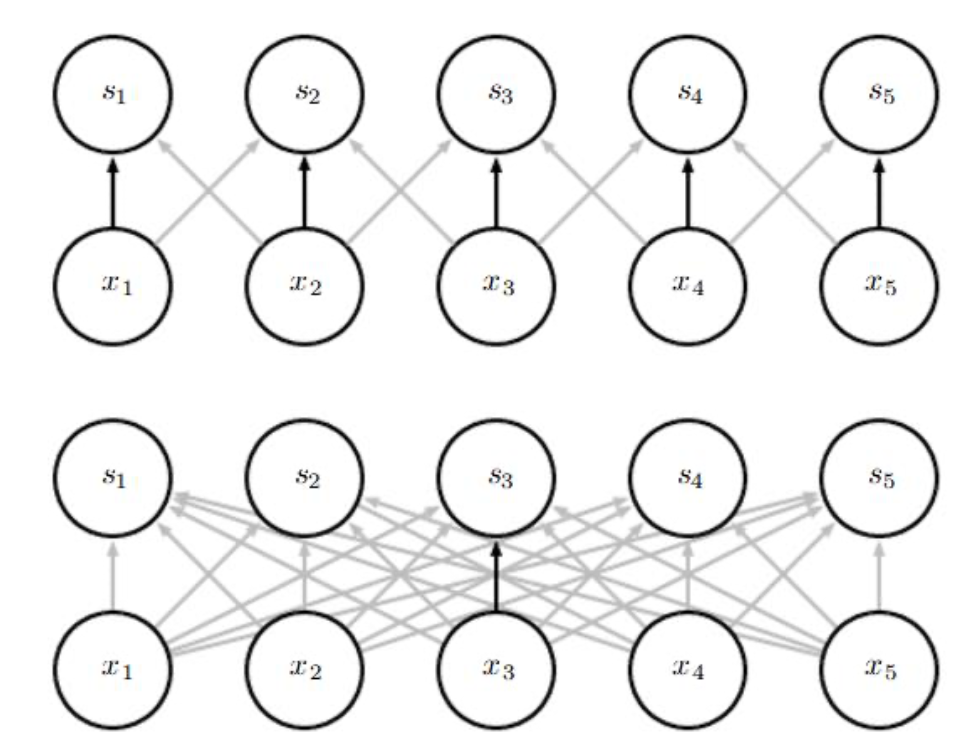
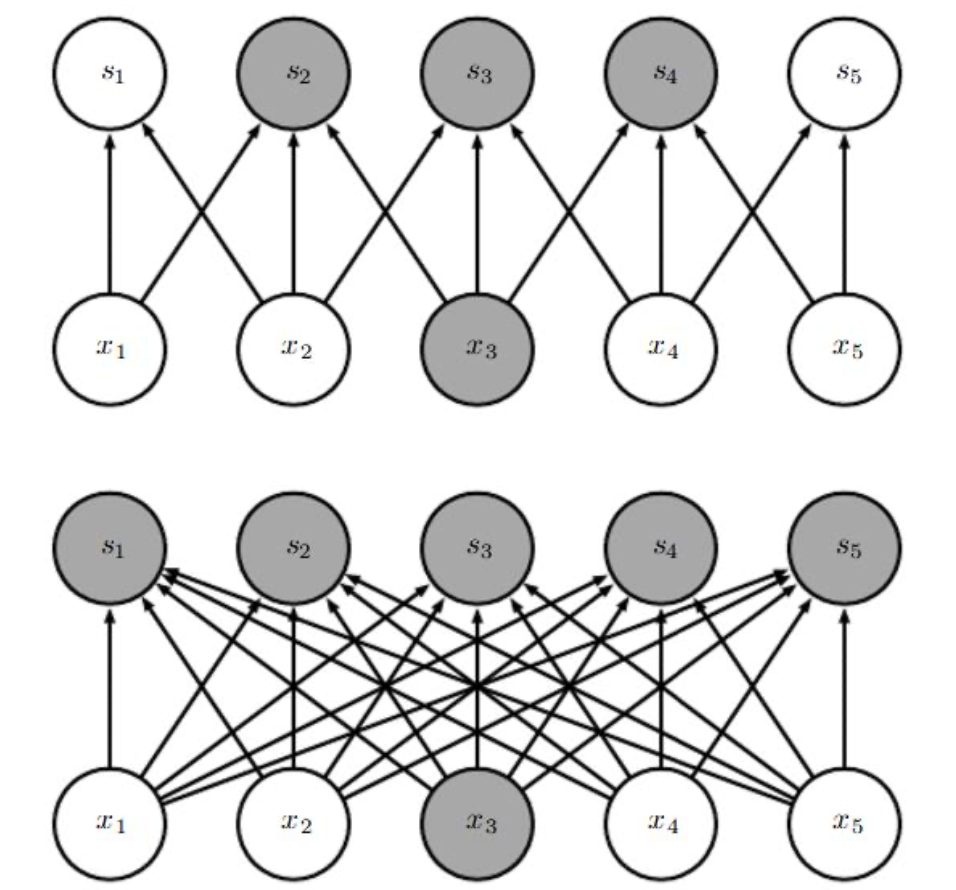
Convolution은 머신러닝 시스템을 향상시킬 수 있는 세 가지 중요한 아이디어를 활용한다. 각각은 sparse interactions, parameter sharing, equivariant representations 이다. 컨볼루션 네트워크는 주로 sparse interaction을 가진다. sparse interaction은 sparse connectivity 또는 sparse weights라고도 한다. 이것은 커널(kernel)을 인풋보다 작게 함으로써 이루어진다. 즉, 더 적은 파라미터를 저장해야한다는 의미이다. 또한, 아웃풋을 계산하기위해 더 적은 작업(operations)이 요구된다는 것이다.
아래 오른쪽의 이미지는 원본 사진의 각 픽셀을 취해 왼쪽의 인접 픽셀의 값을 빼면서 만들어졌다. 두 이미지 모두 280 픽셀이며 입력 이미지는 320 픽셀인 반면 출력 이미지는 319 픽셀이다. 이 변환은 두 개의 요소를 포함하는 컨볼루션 커널로 설명될 수 있고 319*280*3 = 267,960의 floating-point(부동 소수점, CPU의 성능을 수치로 나타낼 때 사용되는 단위) 연산이 요구된다. 행렬곱으로 동일한 변환을 설명하려면 320*280*319*280 또는 80억 이상의 entries가 필요하다.

parameter sharing의 특정한 형태는 레이어가 해석(translation)에 동일성(equivariance)이라 불리는 특성을 갖도록 한다. 함수가 동일하다고 말하는 것은 입력이 바뀌면 출력이 같은 방식으로 바뀐다는 것을 의미한다. 구체적으로 함수 $f(x)$는 $f(g(x)) = g(f(x))$이라면 함수 $g$와 동일하다. convolution의 경우 만약 $g$가 인풋을 해석하는 어떤 함수라면 convolution 함수는 $g$와 동일해진다. 만약 인풋에 있는 객체를 움직이면, 인풋의 representation은 아웃풋에서 같은 양만큼 움직일 것이다. 그러나 Convolution은 이미지의 크기(scale) 변화나 회전 등의 변형과는 동일시 되지 않는다.


아래 오른쪽의 이미지는 원본 사진의 각 픽셀을 취해 왼쪽의 인접 픽셀의 값을 빼면서 만들어졌다. 두 이미지 모두 280 픽셀이며 입력 이미지는 320 픽셀인 반면 출력 이미지는 319 픽셀이다. 이 변환은 두 개의 요소를 포함하는 컨볼루션 커널로 설명될 수 있고 319*280*3 = 267,960의 floating-point(부동 소수점, CPU의 성능을 수치로 나타낼 때 사용되는 단위) 연산이 요구된다. 행렬곱으로 동일한 변환을 설명하려면 320*280*319*280 또는 80억 이상의 entries가 필요하다.

parameter sharing의 특정한 형태는 레이어가 해석(translation)에 동일성(equivariance)이라 불리는 특성을 갖도록 한다. 함수가 동일하다고 말하는 것은 입력이 바뀌면 출력이 같은 방식으로 바뀐다는 것을 의미한다. 구체적으로 함수 $f(x)$는 $f(g(x)) = g(f(x))$이라면 함수 $g$와 동일하다. convolution의 경우 만약 $g$가 인풋을 해석하는 어떤 함수라면 convolution 함수는 $g$와 동일해진다. 만약 인풋에 있는 객체를 움직이면, 인풋의 representation은 아웃풋에서 같은 양만큼 움직일 것이다. 그러나 Convolution은 이미지의 크기(scale) 변화나 회전 등의 변형과는 동일시 되지 않는다.