일반화 (Generalization)
머신러닝에서는 이미 훈련된 모델에 사용된 입력값 뿐만 아니라 새로운 입력값에 대해서도 모델이 잘 작동하도록 하는 것이 중요하다. 새로운 입력값에도 모델이 잘 작동하는 능력을 일반화라고 한다. 최적화와 구분하여 머신 러닝에서는 test error라고도 불리는 generalization error(일반화 오류)가 낮기를 원한다. 따라서 트레이닝 에러뿐만 아니라 테스트 에러에 대한 주의도 필요하다.
훈련 데이터와 테스트 데이터는 data generating process(데이터 생성 과정)라 불리는 데이터셋에 대한 확률분포에 의해 생성된다. 일반적으로 i.i.d 가정을 사용한다. i.i.d 가정이란 independent(독립), identically distributed(동일한 분포)를 뜻한다. 즉, 각각의 데이터셋은 독립이고 훈련 집합과 테스트 집합은 같은 확률 분포에서 나와 동일한 분포를 가진다는 것이다. 이 가정은 확률 분포로 데이터 생성 과정을 설명할 수 있게 해주며 모든 훈련 예제와 테스트 예제를 생성하기 위해 동일한 분포가 사용된다. 데이터 생성 분포를 공유한 것을 $p_{data}$라 부르고 이러한 확률적 체계와 i.i.d 가정은 트레이닝 에러와 테스트 에러 사이의 관계를 수학적으로 연구할 수 있게 해준다.
저적합 및 과적합 (Underfitting and Overfitting)
머신러닝 알고리즘이 얼마나 잘 작동하는지 결정하는 요소는 다음과 같다.
용량 (Capacity)
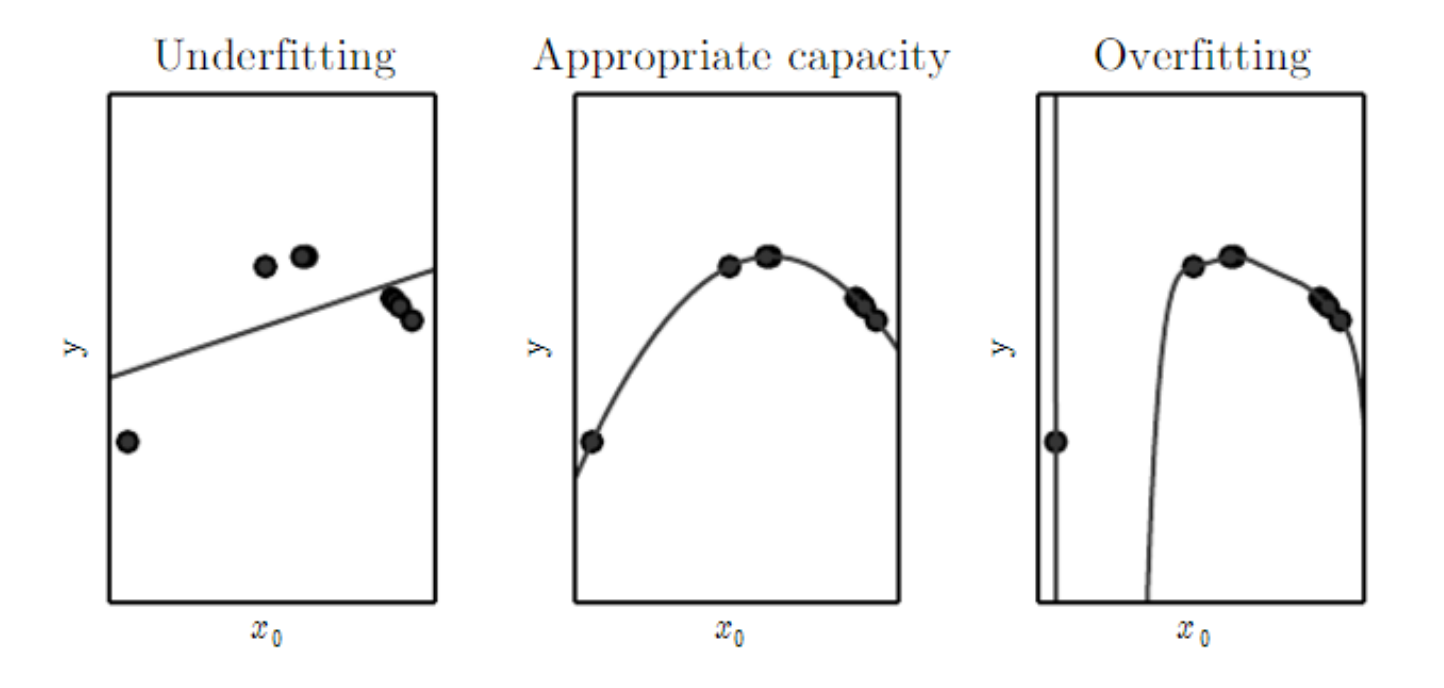
머신러닝에서 모델에 있는 학습 파라미터의 수를 모델의 capacity라고 한다. capacity를 변경함으로써 모델의 적합 정도를 조절할 수 있고 capacity가 높아질수록 트레이닝 셋에 점점 맞춰지기 때문에 과적합될 가능성이 높아진다. 학습 알고리즘의 capacity는 솔루션으로 선택할 수 있는 함수의 집합인 가설 공간(hypothesis space)을 선택함으로써 제어할 수도 있다. 예를 들어 선형 함수가 아닌 다항식(polynomials)을 가설공간에 포함하여 선형 회귀를 일반화 할 수 있다. 이 경우에는 모델의 capacity가 증가한다.
머신러닝 알고리즘은 일반적으로 task의 복잡성과 제공된 트레이닝 데이터의 양에 대한 capacity가 적절할 때 가장 잘 수행된다. capacity가 충분하지 않은 모델은 복잡한 task를 풀 수 없다. capacity가 높은 모델은 복잡한 task는 풀지만 필요 이상으로 capacity가 많아지면 과적합된다.
일반화와 용량 (Generalization and Capacity)
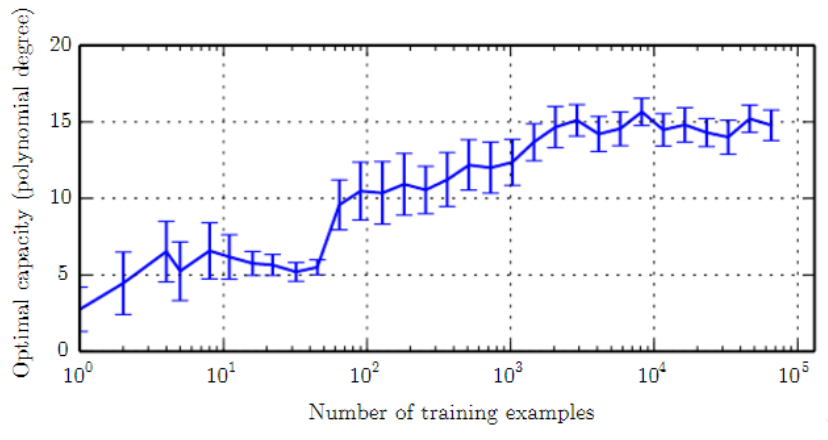
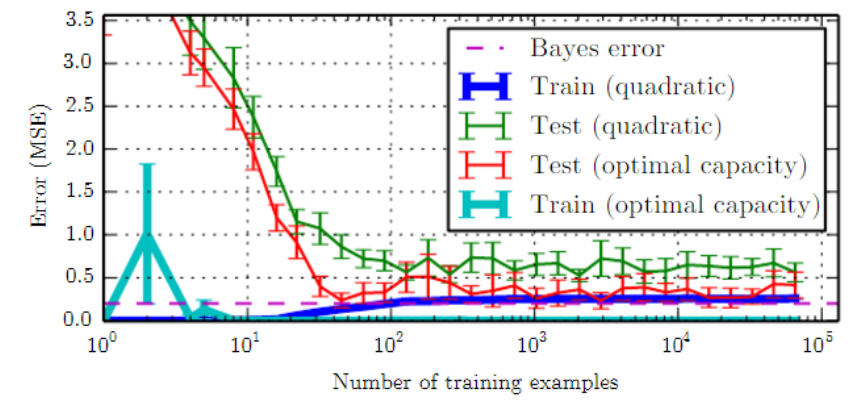
단순한 함수들은 일반화될 가능성이 더 높지만 낮은 트레이닝 에러를 얻기 위해서는 충분히 복잡한 가설을 선택해야 한다. 일반적으로 트레이닝 에러는 모델 capacity가 증가함에 따라 가능한 최소 에러에 근접할 때까지 줄어든다. 일반화 에러는 모델 capacity의 함수로써 U자형 커브 모양을 가진다.
트레이닝 에러와 일반화 에러는 트레이닝셋의 크기에 따라 달라진다. 기대되는(expected) 일반화 에러는 트레이닝 example의 수가 증가한다고 증가할 수 없다. 비모수적 모델에서는 데이터가 많을수록 가능한 가장 좋은 에러를 얻을 때까지 더 좋은 일반화를 만든다. 최적 capacity보다 작은 어떤 고정된 모수 모델은 베이즈 에러를 초과하는 에러값에 근접할 것이다. 모델은 최적의 capacity를 가질 수 있지만 여전히 트레이닝 에러와 일반화 에러 사이의 큰 차이를 가진다.
No Free Lunch Theorem
'공짜 점심은 없다' 라는 이론은 머신러닝 알고리즘이 다른 어떤 것보다 일반적으로 낫지 않음을 뜻한다. 즉, 머신러닝이 만능은 아니라는 것이다. 모든 분류 알고리즘은 이전에 관찰되지 않은 point를 분류할 때, 가능한 모든 데이터 생성 분포에 대한 평균으로써 동일한 오류 비율을 가진다. 다행히도 이런 결과는 가능한 모든 데이터 생성 분포에 대해 평균을 낼 때만 유지되므로 실제 응용사례에서 접하는 확률 분포의 종류에 대한 가정을 만들면, 이러한 분포에서 잘 수행되는 학습 알고리즘을 설계할 수 있다.
머신러닝 연구의 목표는 일반적인 학습 알고리즘이나 절대적으로 가장 좋은 학습 알고리즘을 찾는 것이 아니다. 대신, AI 에이전트가 경험하는 실제 세계와 어떤 분포가 관련되는지 이해하고 우리가 관심을 갖는 분포에서 도출된 데이터로부터 어떤 종류의 머신러닝 알고리즘이 잘 수행되는지 파악하는 것이다.
정규화 (Regularization)
No Free Lunch Theorem은 머신러닝 알고리즘이 구체적인 task를 잘 수행하도록 디자인 해야함을 시사한다. 지금까지 학습 알고리즘을 수정하는 유일한 방법은 솔루션의 가설 공간에 함수를 추가하거나 제거함으로써 모델의 표현 용량을 증가시키거나 감소시키는 것이었다. 어떤 종류의 함수에서 솔루션을 도출할 수 있게 선택하고 이러한 함수의 양을 조절함으로써 알고리즘의 성능을 제어할 수 있다.
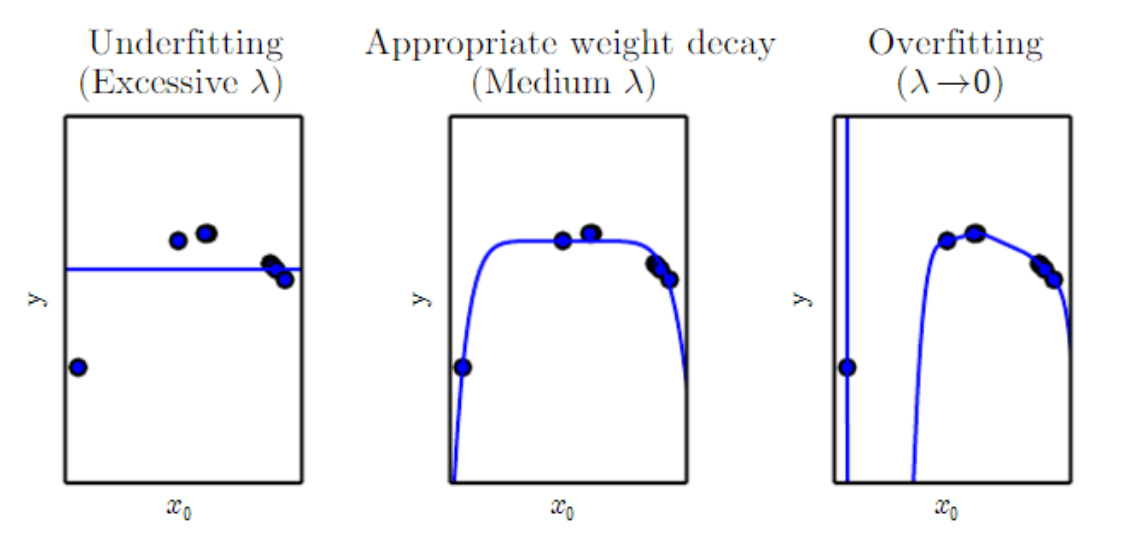
또한 가설 공간에서 다른곳으로 하나의 솔루션에 대한 선호도(preference)를 줄 수 있다. 예를 들어 weight decay ($J(w)=MSE_{train} + \lambda w^Tw$) 가 있다. 트레이닝 데이터 적합에 대한 가중치를 선택할 수 있는 것인데 weight decay의 값이 커질수록 가중치 값이 작아져 과적합 현상을 해소할 수 있지만, weight decay 값을 너무 크게 하면 저적합 현상이 발생하므로 적당한 값을 사용해야 한다. 좀더 일반적으로 함수 $f(x;\theta)$ 를 비용함수에 정규화(regularizer)라 불리는 패널티로 추가해줌으로써 모델을 정규화할 수 있다. weight decay의 경우 regularizer는 $\Omega (w) = w^Tw$ 이다.
머신러닝에서는 이미 훈련된 모델에 사용된 입력값 뿐만 아니라 새로운 입력값에 대해서도 모델이 잘 작동하도록 하는 것이 중요하다. 새로운 입력값에도 모델이 잘 작동하는 능력을 일반화라고 한다. 최적화와 구분하여 머신 러닝에서는 test error라고도 불리는 generalization error(일반화 오류)가 낮기를 원한다. 따라서 트레이닝 에러뿐만 아니라 테스트 에러에 대한 주의도 필요하다.
훈련 데이터와 테스트 데이터는 data generating process(데이터 생성 과정)라 불리는 데이터셋에 대한 확률분포에 의해 생성된다. 일반적으로 i.i.d 가정을 사용한다. i.i.d 가정이란 independent(독립), identically distributed(동일한 분포)를 뜻한다. 즉, 각각의 데이터셋은 독립이고 훈련 집합과 테스트 집합은 같은 확률 분포에서 나와 동일한 분포를 가진다는 것이다. 이 가정은 확률 분포로 데이터 생성 과정을 설명할 수 있게 해주며 모든 훈련 예제와 테스트 예제를 생성하기 위해 동일한 분포가 사용된다. 데이터 생성 분포를 공유한 것을 $p_{data}$라 부르고 이러한 확률적 체계와 i.i.d 가정은 트레이닝 에러와 테스트 에러 사이의 관계를 수학적으로 연구할 수 있게 해준다.
저적합 및 과적합 (Underfitting and Overfitting)
머신러닝 알고리즘이 얼마나 잘 작동하는지 결정하는 요소는 다음과 같다.
- 트레이닝 에러가 작은가
- 트레이닝 에러와 테스트 에러 사이의 차이가 작은가
용량 (Capacity)
머신러닝에서 모델에 있는 학습 파라미터의 수를 모델의 capacity라고 한다. capacity를 변경함으로써 모델의 적합 정도를 조절할 수 있고 capacity가 높아질수록 트레이닝 셋에 점점 맞춰지기 때문에 과적합될 가능성이 높아진다. 학습 알고리즘의 capacity는 솔루션으로 선택할 수 있는 함수의 집합인 가설 공간(hypothesis space)을 선택함으로써 제어할 수도 있다. 예를 들어 선형 함수가 아닌 다항식(polynomials)을 가설공간에 포함하여 선형 회귀를 일반화 할 수 있다. 이 경우에는 모델의 capacity가 증가한다.
머신러닝 알고리즘은 일반적으로 task의 복잡성과 제공된 트레이닝 데이터의 양에 대한 capacity가 적절할 때 가장 잘 수행된다. capacity가 충분하지 않은 모델은 복잡한 task를 풀 수 없다. capacity가 높은 모델은 복잡한 task는 풀지만 필요 이상으로 capacity가 많아지면 과적합된다.
일반화와 용량 (Generalization and Capacity)
단순한 함수들은 일반화될 가능성이 더 높지만 낮은 트레이닝 에러를 얻기 위해서는 충분히 복잡한 가설을 선택해야 한다. 일반적으로 트레이닝 에러는 모델 capacity가 증가함에 따라 가능한 최소 에러에 근접할 때까지 줄어든다. 일반화 에러는 모델 capacity의 함수로써 U자형 커브 모양을 가진다.
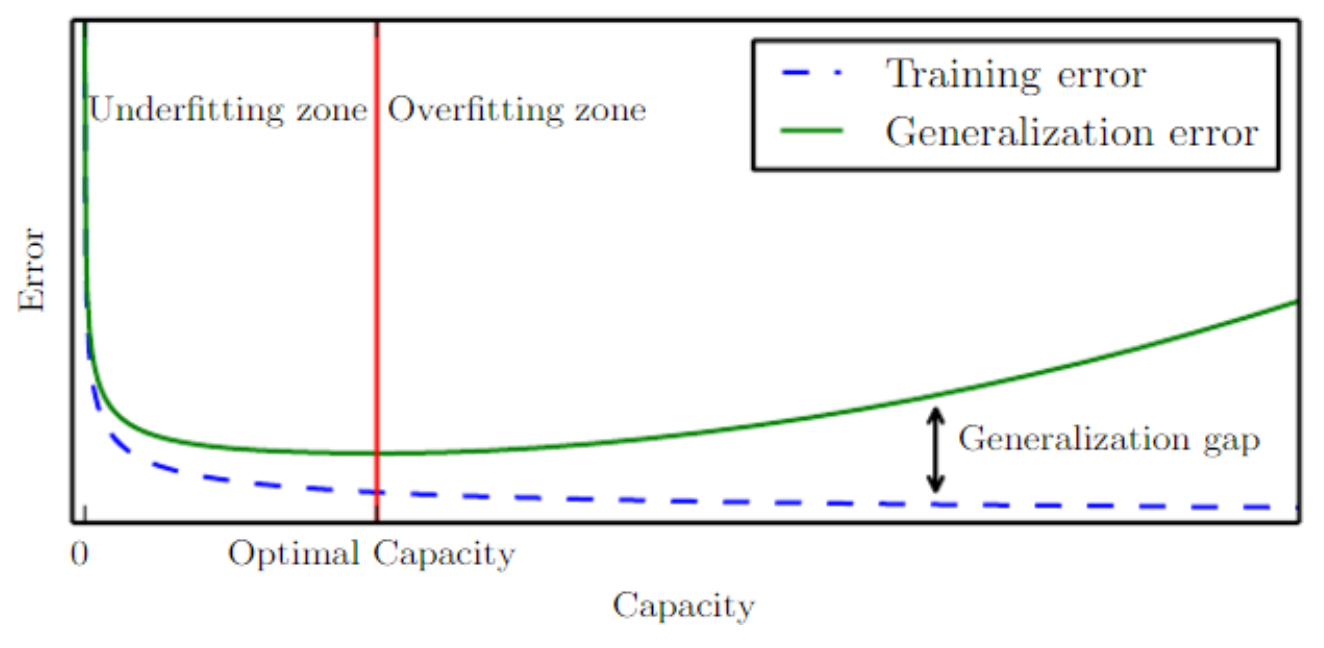
트레이닝 에러와 일반화 에러는 트레이닝셋의 크기에 따라 달라진다. 기대되는(expected) 일반화 에러는 트레이닝 example의 수가 증가한다고 증가할 수 없다. 비모수적 모델에서는 데이터가 많을수록 가능한 가장 좋은 에러를 얻을 때까지 더 좋은 일반화를 만든다. 최적 capacity보다 작은 어떤 고정된 모수 모델은 베이즈 에러를 초과하는 에러값에 근접할 것이다. 모델은 최적의 capacity를 가질 수 있지만 여전히 트레이닝 에러와 일반화 에러 사이의 큰 차이를 가진다.


No Free Lunch Theorem
'공짜 점심은 없다' 라는 이론은 머신러닝 알고리즘이 다른 어떤 것보다 일반적으로 낫지 않음을 뜻한다. 즉, 머신러닝이 만능은 아니라는 것이다. 모든 분류 알고리즘은 이전에 관찰되지 않은 point를 분류할 때, 가능한 모든 데이터 생성 분포에 대한 평균으로써 동일한 오류 비율을 가진다. 다행히도 이런 결과는 가능한 모든 데이터 생성 분포에 대해 평균을 낼 때만 유지되므로 실제 응용사례에서 접하는 확률 분포의 종류에 대한 가정을 만들면, 이러한 분포에서 잘 수행되는 학습 알고리즘을 설계할 수 있다.
머신러닝 연구의 목표는 일반적인 학습 알고리즘이나 절대적으로 가장 좋은 학습 알고리즘을 찾는 것이 아니다. 대신, AI 에이전트가 경험하는 실제 세계와 어떤 분포가 관련되는지 이해하고 우리가 관심을 갖는 분포에서 도출된 데이터로부터 어떤 종류의 머신러닝 알고리즘이 잘 수행되는지 파악하는 것이다.
정규화 (Regularization)
No Free Lunch Theorem은 머신러닝 알고리즘이 구체적인 task를 잘 수행하도록 디자인 해야함을 시사한다. 지금까지 학습 알고리즘을 수정하는 유일한 방법은 솔루션의 가설 공간에 함수를 추가하거나 제거함으로써 모델의 표현 용량을 증가시키거나 감소시키는 것이었다. 어떤 종류의 함수에서 솔루션을 도출할 수 있게 선택하고 이러한 함수의 양을 조절함으로써 알고리즘의 성능을 제어할 수 있다.
또한 가설 공간에서 다른곳으로 하나의 솔루션에 대한 선호도(preference)를 줄 수 있다. 예를 들어 weight decay ($J(w)=MSE_{train} + \lambda w^Tw$) 가 있다. 트레이닝 데이터 적합에 대한 가중치를 선택할 수 있는 것인데 weight decay의 값이 커질수록 가중치 값이 작아져 과적합 현상을 해소할 수 있지만, weight decay 값을 너무 크게 하면 저적합 현상이 발생하므로 적당한 값을 사용해야 한다. 좀더 일반적으로 함수 $f(x;\theta)$ 를 비용함수에 정규화(regularizer)라 불리는 패널티로 추가해줌으로써 모델을 정규화할 수 있다. weight decay의 경우 regularizer는 $\Omega (w) = w^Tw$ 이다.