정규화는 딥러닝의 출현 이전에도 수십년 동안 사용되어 왔다. 선형 회귀모형이나 로지스틱 회귀모형 같은 선형 모델은 간단하고 효과적인 정규화가 가능하다. 많은 정규화 방법은 목적함수 $J$에 파라미터 norm penalty $\Omega(\theta)$를 추가하여 모델의 capacity를 제한하는 것에 기초한다. 정규화된 목적함수는 다음과 같다.
$L^2$ Parameter Regularization
$L^2$ parameter norm penalty는 흔히 weight decay로 알려져 있다. $$ \begin{array}{c}\Omega(\boldsymbol{\theta})=\frac{1}{2}\|\boldsymbol{w}\|_{2}^{2} \\ \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\frac{\alpha}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y}) \\ \nabla_{\boldsymbol{w}} \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\alpha \boldsymbol{w}+\nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})\end{array} $$ single gradient step을 수행하여 가중치를 업데이트 하는 방법은 다음과 같다. $$ \begin{array}{l}\boldsymbol{w} \leftarrow \boldsymbol{w}-\epsilon\left(\alpha \boldsymbol{w}+\nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})\right) \\ \boldsymbol{w} \leftarrow(1-\epsilon \alpha) \boldsymbol{w}-\epsilon \nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})\end{array} $$ 정규화되지 않은 트레이닝 비용을 최소화하는 가중치 값과 인접한 목적 함수에 대한 2차(quadratic) 근사를 만들어 분석을 단순하게 할 수 있다. 여기서 $H$는 $w^*$에서 평가된 $w$에 관한 $J$의 헤시안(Hessian) 행렬이다. $$ \begin{aligned} &\boldsymbol{w}^{*}=\arg \min _{\boldsymbol{w}} J(\boldsymbol{w}) \\ &\hat{J}(\boldsymbol{\theta}) =J\left(\boldsymbol{w}^{*}\right)+\frac{1}{2}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right)^{\top} \boldsymbol{H}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right) \end{aligned} $$ gradient가 0일 때 $\hat{J}$가 최소가 된다. $$ \nabla_{\boldsymbol{w}} \hat{J}(\boldsymbol{w})=\boldsymbol{H}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right) $$ 이제 정규화된 $\hat{J}$의 최소값을 다음과 같이 구할 수 있게 된다. $$ \begin{array}{c}\alpha \tilde{\boldsymbol{w}}+\boldsymbol{H}\left(\tilde{\boldsymbol{w}}-\boldsymbol{w}^{*}\right)=0 \\ (\boldsymbol{H}+\alpha \boldsymbol{I}) \tilde{\boldsymbol{w}}=\boldsymbol{H} \boldsymbol{w}^{*} \\ \tilde{\boldsymbol{w}}=(\boldsymbol{H}+\alpha \boldsymbol{I})^{-1} \boldsymbol{H} \boldsymbol{w}^{*}\end{array} $$ $\boldsymbol{H}=Q \Lambda Q^{\top}$로 분해(decompose) 할 수 있다. $$ \begin{aligned} \tilde{w} &=\left(Q \Lambda Q^{\top}+\alpha I\right)^{-1} Q \Lambda Q^{\top} w^{*} \\ &=\left[Q(\Lambda+\alpha I) Q^{\top}\right]^{-1} Q \Lambda Q^{\top} w^{*} \\ &=Q(\Lambda+\alpha I)^{-1} \Lambda Q^{\top} w^{*} \end{aligned} $$ weight decay의 효과는 $\boldsymbol{H}$의 고유벡터(eigenvector)로 정의된 축을 따라서 $w^{*}$를 rescale하는 것이다. $\boldsymbol{H}$의 i번째 고유벡터로 정렬된 $w^*$의 성분은 $\lambda_i / (\lambda_i+\alpha)$ 의 인수로 재조정된다. $\boldsymbol{H}$의 고유값(eigenvalue)이 상대적으로 큰 방향을 따르면 (ex. $\lambda_i >> \alpha$) 정규화의 효과는 상대적으로 작아진다. 그러나 $\lambda_i << \alpha$인 성분의 크기는 거의 0에 가까울 정도로 줄어들 것이다.
$L^2$ weight decay가 weight decay의 가장 흔한 형식인 반면에, 모델 파라미터의 사이즈를 패널라이즈(penalize)하는 다른 방법도 있다. 그것은 바로 다음과 같이 $L^1$ 정규화를 사용하는 것이다. $$ \begin{array}{c}\Omega(\boldsymbol{\theta})=\|\boldsymbol{w}\|_{1}=\sum\left|w_{i}\right| \\ \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\alpha\|\boldsymbol{w}\|_{1}+J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y}) \\ \nabla_{w} \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\alpha \operatorname{sign}(\boldsymbol{w})+\nabla_{w} J(\boldsymbol{X}, y ; \boldsymbol{w})\end{array} $$ $H=\operatorname{diag}\left(\left[H_{1,1}, \ldots, H_{n, n}\right]\right)$와 같이 헤시안이 대각(diagonal)이라는 더욱 간단한 가정을 한다. 이 가정은 입력 특징들 사이의 모든 상관관계(correlation)를 제거하기 위해 선형회귀 문제에 대한 데이터가 전처리된 경우에 적용된다.
$L^1$ 정규화된 목적 함수의 2차 근사는 다음과 같이 파라미터에 걸쳐 합(sum)으로 분해된다. $$ \hat{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=J\left(\boldsymbol{w}^{*} ; \boldsymbol{X}, \boldsymbol{y}\right)+\sum_{i}\left[\frac{1}{2} H_{i, i}\left(\boldsymbol{w}_{i}-\boldsymbol{w}_{i}^{*}\right)^{2}+\alpha\left|w_{i}\right|\right] $$ 비용함수의 근사를 최소화하는 문제는 다음과 같은 형태로 각 차원 $i$에 대한 분석적인 솔루션을 가진다. $$ w_{i}=\operatorname{sign}\left(w_{i}^{*}\right) \max \left\{\left|w_{i}^{*}\right|-\frac{\alpha}{H_{i, i}}, 0\right\} $$ 모든 $i$에 대해 $w^*_i > 0$인 상황을 고려해보자.
$$ \tilde{J}(\boldsymbol{\theta} ; \boldsymbol{X}, \boldsymbol{y})=J(\boldsymbol{\theta} ; \boldsymbol{X}, \boldsymbol{y})+\alpha \Omega(\boldsymbol{\theta}), \quad \text { where } \alpha \in[0, \infty) $$
$\alpha$를 0으로 설정하면 정규화가 되지 않고 $\alpha$의 값이 클수록 더 정규화된다. parameter norm $\Omega$에 대해 다른 솔루션이 더 선호될 수 있다. 일반적으로 각 계층에서 affine 변환의 가중치에 대해서만 패널티를 주고 편차(bias)를 정규화하지 않는 파라미터 norm penalty $\Omega$를 사용한다. 편차를 정확하게 fit하기 위해 가중치보다 더 적은 데이터가 필요하고 편차 파라미터 정규화는 상당한 underfitting 양을 도입할 수 있다.$L^2$ Parameter Regularization
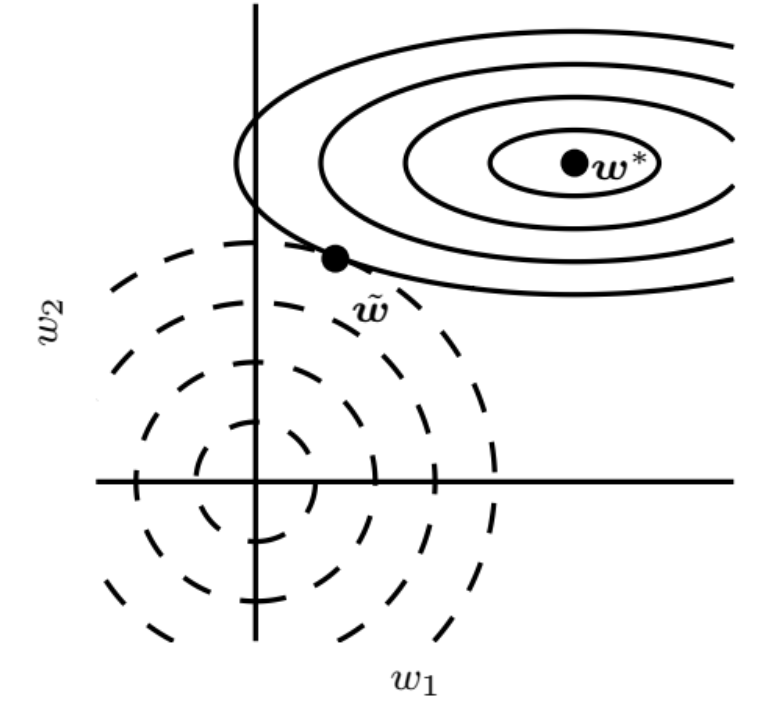
$L^2$ parameter norm penalty는 흔히 weight decay로 알려져 있다. $$ \begin{array}{c}\Omega(\boldsymbol{\theta})=\frac{1}{2}\|\boldsymbol{w}\|_{2}^{2} \\ \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\frac{\alpha}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y}) \\ \nabla_{\boldsymbol{w}} \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\alpha \boldsymbol{w}+\nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})\end{array} $$ single gradient step을 수행하여 가중치를 업데이트 하는 방법은 다음과 같다. $$ \begin{array}{l}\boldsymbol{w} \leftarrow \boldsymbol{w}-\epsilon\left(\alpha \boldsymbol{w}+\nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})\right) \\ \boldsymbol{w} \leftarrow(1-\epsilon \alpha) \boldsymbol{w}-\epsilon \nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})\end{array} $$ 정규화되지 않은 트레이닝 비용을 최소화하는 가중치 값과 인접한 목적 함수에 대한 2차(quadratic) 근사를 만들어 분석을 단순하게 할 수 있다. 여기서 $H$는 $w^*$에서 평가된 $w$에 관한 $J$의 헤시안(Hessian) 행렬이다. $$ \begin{aligned} &\boldsymbol{w}^{*}=\arg \min _{\boldsymbol{w}} J(\boldsymbol{w}) \\ &\hat{J}(\boldsymbol{\theta}) =J\left(\boldsymbol{w}^{*}\right)+\frac{1}{2}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right)^{\top} \boldsymbol{H}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right) \end{aligned} $$ gradient가 0일 때 $\hat{J}$가 최소가 된다. $$ \nabla_{\boldsymbol{w}} \hat{J}(\boldsymbol{w})=\boldsymbol{H}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right) $$ 이제 정규화된 $\hat{J}$의 최소값을 다음과 같이 구할 수 있게 된다. $$ \begin{array}{c}\alpha \tilde{\boldsymbol{w}}+\boldsymbol{H}\left(\tilde{\boldsymbol{w}}-\boldsymbol{w}^{*}\right)=0 \\ (\boldsymbol{H}+\alpha \boldsymbol{I}) \tilde{\boldsymbol{w}}=\boldsymbol{H} \boldsymbol{w}^{*} \\ \tilde{\boldsymbol{w}}=(\boldsymbol{H}+\alpha \boldsymbol{I})^{-1} \boldsymbol{H} \boldsymbol{w}^{*}\end{array} $$ $\boldsymbol{H}=Q \Lambda Q^{\top}$로 분해(decompose) 할 수 있다. $$ \begin{aligned} \tilde{w} &=\left(Q \Lambda Q^{\top}+\alpha I\right)^{-1} Q \Lambda Q^{\top} w^{*} \\ &=\left[Q(\Lambda+\alpha I) Q^{\top}\right]^{-1} Q \Lambda Q^{\top} w^{*} \\ &=Q(\Lambda+\alpha I)^{-1} \Lambda Q^{\top} w^{*} \end{aligned} $$ weight decay의 효과는 $\boldsymbol{H}$의 고유벡터(eigenvector)로 정의된 축을 따라서 $w^{*}$를 rescale하는 것이다. $\boldsymbol{H}$의 i번째 고유벡터로 정렬된 $w^*$의 성분은 $\lambda_i / (\lambda_i+\alpha)$ 의 인수로 재조정된다. $\boldsymbol{H}$의 고유값(eigenvalue)이 상대적으로 큰 방향을 따르면 (ex. $\lambda_i >> \alpha$) 정규화의 효과는 상대적으로 작아진다. 그러나 $\lambda_i << \alpha$인 성분의 크기는 거의 0에 가까울 정도로 줄어들 것이다.
$L^2$ weight decay가 weight decay의 가장 흔한 형식인 반면에, 모델 파라미터의 사이즈를 패널라이즈(penalize)하는 다른 방법도 있다. 그것은 바로 다음과 같이 $L^1$ 정규화를 사용하는 것이다. $$ \begin{array}{c}\Omega(\boldsymbol{\theta})=\|\boldsymbol{w}\|_{1}=\sum\left|w_{i}\right| \\ \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\alpha\|\boldsymbol{w}\|_{1}+J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y}) \\ \nabla_{w} \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\alpha \operatorname{sign}(\boldsymbol{w})+\nabla_{w} J(\boldsymbol{X}, y ; \boldsymbol{w})\end{array} $$ $H=\operatorname{diag}\left(\left[H_{1,1}, \ldots, H_{n, n}\right]\right)$와 같이 헤시안이 대각(diagonal)이라는 더욱 간단한 가정을 한다. 이 가정은 입력 특징들 사이의 모든 상관관계(correlation)를 제거하기 위해 선형회귀 문제에 대한 데이터가 전처리된 경우에 적용된다.
$L^1$ 정규화된 목적 함수의 2차 근사는 다음과 같이 파라미터에 걸쳐 합(sum)으로 분해된다. $$ \hat{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=J\left(\boldsymbol{w}^{*} ; \boldsymbol{X}, \boldsymbol{y}\right)+\sum_{i}\left[\frac{1}{2} H_{i, i}\left(\boldsymbol{w}_{i}-\boldsymbol{w}_{i}^{*}\right)^{2}+\alpha\left|w_{i}\right|\right] $$ 비용함수의 근사를 최소화하는 문제는 다음과 같은 형태로 각 차원 $i$에 대한 분석적인 솔루션을 가진다. $$ w_{i}=\operatorname{sign}\left(w_{i}^{*}\right) \max \left\{\left|w_{i}^{*}\right|-\frac{\alpha}{H_{i, i}}, 0\right\} $$ 모든 $i$에 대해 $w^*_i > 0$인 상황을 고려해보자.
- $w^*_i \le \alpha / H_{i,i}$인 경우
여기서 $w_i = 0$ 이다. 정규화된 목적함수에 대한 $J(w;X,y)$의 contribution이 $L^1$ 정규화에 의해 $i$ 방향으로 overwhelmed 되기 때문에 발생한다. - $w^*_i > \alpha / H_{i,i}$인 경우
이 경우는 정규화가 $w_i$의 최적값을 0으로 이동시키는 것이 아니라 $\alpha H_{i,i}$와 같은 거리만큼 그 방향으로만 이동시킨다.