Dropout은 광범위한 모델 family를 정규화하는 계산적으로 효율적이고 강력한 방법을 제공한다. 드랍아웃은 매우 큰 신경망의 앙상블(ensembles)에 실용적인 bagging을 만드는 방법이라고 생각할 수 있다. Bagging은 다수의 모델을 훈련시키고 각 테스트 예제에서 다양한 모델을 평가하는 것을 포함한다. 그러나 각 모델이 큰 신경망일 때, 네트워크를 훈련하고 평가하는 것은 실행시간과 메모리 관점에서 비용이 많이 들기 때문에 비현실적으로 보인다. 그래서 5개~10개 사이의 신경망의 앙상블을 사용하는 것이 일반적이다. 드랍아웃은 기하급수적으로 많은 신경망의 bagged 앙상블을 훈련하고 평가하는데 inexpensive한 근사를 제공한다.
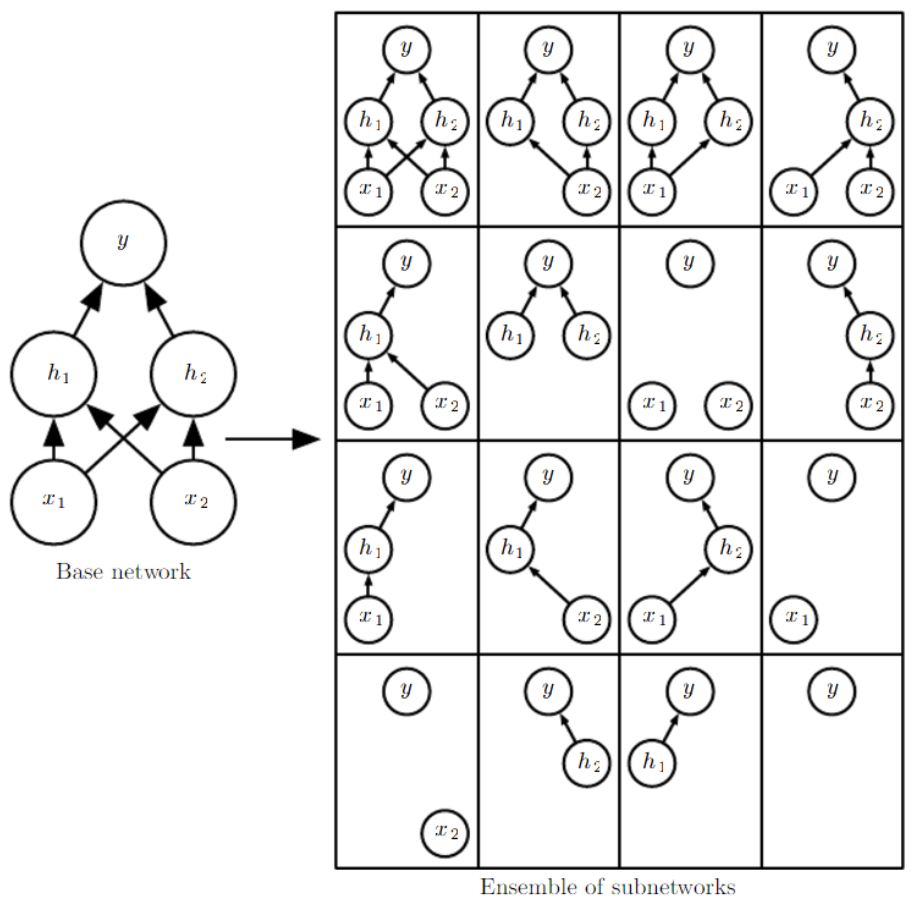
드랍아웃은 기본 네트워크에서 출력되지 않는 단위를 제거함으로써 만들 수 있는 모든 하위네트워크(subnetworks)로 구성된 앙상블을 훈련시킨다. 그 출력값에 0을 곱하면 네트워크에서 한 단위를 효과적으로 제거할 수 있다. 드랍아웃으로 트레이닝하기 위해 stochastic gradient descent와 같은 작은 스텍을 만드는 minibatch 기반 학습알고리즘을 사용한다. minibatch에 example을 load할 때마다, 네트워크의 모든 입력 단위와 숨겨진(hidden) 단위에 적용하기 위해 다른 binary mask를 무작위로 샘플링한다. 1의 mask 값을 샘플링할 확률은 훈련을 시작하기 전에 고정된 하이퍼 파라미터이다. 일반적으로 입력 단위는 0.8의 확률을 사용하고 숨겨진 단위는 0.5의 확률을 사용한다.
Weight Scaling Inference Rule
그러나 훨씬 더 좋은 접근법은 단 하나의 forward 전파(propagation) cost로 전체 앙상블의 예측에 대한 좋은 근사치를 얻을 수 있게 해주는 것이다. 그렇게 하기 위해, 앙상블 멤버의 예측 분포의 산술 평균보다는 기하(geometric) 평균을 사용한다. Warde-Farley et al.(2014) 에서는 기하 평균이 산술 평균과 동등하게 수행된다는 주장과 경험적(empirical) 증거를 제시한다. 정규화되지 않은 확률 분포는 기하평균에 의해 다음과 같이 직접 정의된다. $$ \tilde{p}_{\text {ensemble }}(y | \boldsymbol{x})=\sqrt[2^{d}]{\prod_{\mu} p(y | \boldsymbol{x}, \boldsymbol{\mu})} $$ 여기서 $d$는 dropped 될 수 있는 단위의 수이다. 여기서는 표현을 단순히하기 위해 $\mu$에 대한 균등(uniform) 분포를 사용하지만 불균등(nonuniform) 분포 또한 가능하다. 예측을 하기 위해서는 앙상블을 다음과 같이 renormalize 해야한다. $$ p_{\text {ensemble }}(y | \boldsymbol{x})=\frac{\tilde{p}_{\text {ensemble }}(y | \boldsymbol{x})}{\sum_{y^{\prime}} \tilde{p}_{\text {ensemble }}\left(y^{\prime} | \boldsymbol{x}\right)} $$ $p(y|x)$를 하나의 모델에서 평가함으로써 $p_{\text{ensemble}}$의 근사치를 구할 수 있다. 그 모델은 모든 단위를 포함하지만 단위 $i$를 벗어나는 가중치에 단위 $i$를 포함하는 확률을 곱한 것이다. 이러한 접근법을 weight scaling inference rule 이라 부른다. 깊은 비선형 네트워크에서 이 근사 추론 규칙의 정확성에 대해 아직 이론적인 argument는 없지만 경험적으로 매우 잘 작동된다.
비선형의 hidden units가 없는 모델의 많은 클래스의 경우 weight scaling inference rule이 정확하다. 간단한 예제로, 벡터 $v$로 표현되는 n개의 입력 변수를 가지는 소프트맥스 회귀 분류기는 다음과 같다. $$ P(\mathrm{y}=y | \mathbf{v})=\operatorname{softmax}\left(\boldsymbol{W}^{\top} \mathbf{v}+\boldsymbol{b}\right)_{y} $$ 이항 벡터 $d$를 가지는 인풋의 요소별(element-wise) 곱셈에 의해 하위 모델의 family를 다음과 같이 인덱싱할 수 있다. $$ \begin{align} P(\mathrm{y}=y | \mathrm{v} ; d)=\operatorname{softmax}\left(W^{\top}(d \odot \mathrm{v})+b\right)_{y} \notag\\ P_{\text {ensemble }}(\mathrm{y}=y | \mathbf{v})=\frac{\tilde{P}_{\text {ensemble }}(\mathrm{y}=y | \mathbf{v})}{\sum_{y^{\prime}} \tilde{P}_{\text {ensemble }}\left(\mathrm{y}=y^{\prime} | \mathbf{v}\right)} \notag\\ \tilde{P}_{\text {ensemble }}(\mathrm{y}=y | \mathbf{v})= \sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} P(\mathrm{y}=y | \mathbf{v} ; \mathbf{d})} \notag \end{align} $$ $$ \begin{align} &=\sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \operatorname{softmax}\left(\boldsymbol{W}^{\top}(\boldsymbol{d} \odot \mathbf{v})+\boldsymbol{b}\right)_{y}} \notag\\ &=\sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \frac{\exp \left(\boldsymbol{W}_{y,:}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y}\right)}{\sum_{y^{\prime}} \exp \left(\boldsymbol{W}_{y^{\prime}, :}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y^{\prime}}\right)}} \notag\\ &=\frac{\sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \exp \left(\boldsymbol{W}_{y,:}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y}\right)}}{\sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \sum_{y^{\prime}} \exp \left(\boldsymbol{W}_{y^{\prime},:}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y^{\prime}}\right)}}\notag \\ \end{align} $$ $$ \begin{aligned} \tilde{P}_{\text {ensemble }}(\mathrm{y}=y |&\mathbf{v}) \propto \sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \exp \left(W_{y, i}^{\top}(d \odot \mathrm{v})+b_{y}\right)} \end{aligned} $$ $$ \begin{array}{c}=\exp \left(\frac{1}{2^{n}} \sum_{\boldsymbol{d} \in\{0,1\}^{n}} \boldsymbol{W}_{y,:}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y}\right) \\ =\exp \left(\frac{1}{2} \boldsymbol{W}_{y,:}^{\top} \mathbf{v}+b_{y}\right)\end{array} $$ weight scaling rule은 비선형성이 있는 deep 모델에 대한 근사치일 뿐이다. 비록 근사치가 이론적으로 특징되어지지 않지만, 경험적으로 잘 작동하는 경우가 많다.
Advantages of Dropout
Srivastava et al. (2014)에서는 weight decay, filter norm constraints, sparse activity regularization과 같은 계산적으로 inexpensive한 표준 정규화 방법보다 dropout이 더 효과적이라는 것을 보였다. 드랍아웃의 장점은 계산적으로 매우 cheap하다는 것이다. 트레이닝을 할 때 드랍아웃을 사용하는 것은 example 업데이트당 O(n)계산만 하면 된다. 또한 역전파(back propagation) 단계까지 이진수를 저장하기 위해 O(n) 메모리가 요구된다. 또 다른 중요한 장점은 사용할 수 있는 모델이나 트레이닝 절차의 타입을 제한하지 않는다는 것이다. 분포로 표현한 거의 모든 모델에서 잘 작동하고 stochastic gradient descent로 트레이닝 될 수 있다.
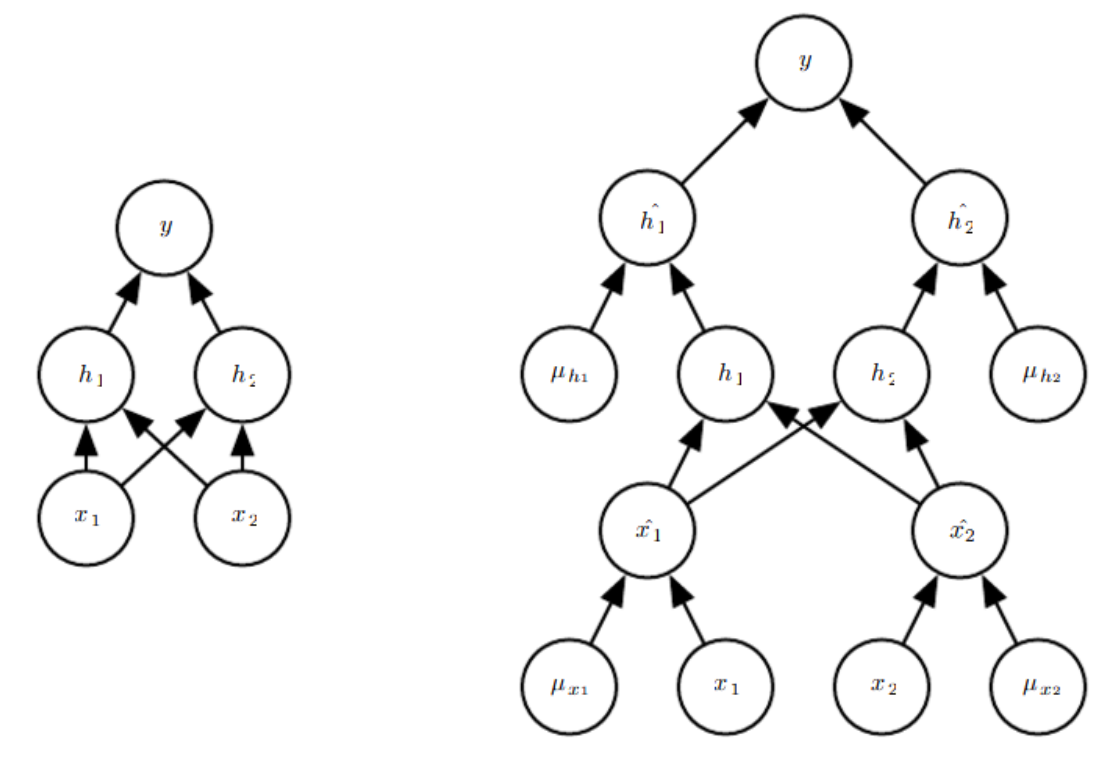
dropout의 상당 부분은 hidden units에 masking noise가 적용된다는 사실에서 발생한다는 점을 이해하는 것이 중요하다. 이것은 입력값의 raw values 보다 information content에 대한 고도의 지능적이고 적응적인 destruction 형태로 볼 수 있다. 원래 값보다 추출된 특징을 파괴하면 destruction 프로세스가 지금까지 획득한 입력 분포에 대한 모든 지식을 사용할 수 있다.
드랍아웃은 기본 네트워크에서 출력되지 않는 단위를 제거함으로써 만들 수 있는 모든 하위네트워크(subnetworks)로 구성된 앙상블을 훈련시킨다. 그 출력값에 0을 곱하면 네트워크에서 한 단위를 효과적으로 제거할 수 있다. 드랍아웃으로 트레이닝하기 위해 stochastic gradient descent와 같은 작은 스텍을 만드는 minibatch 기반 학습알고리즘을 사용한다. minibatch에 example을 load할 때마다, 네트워크의 모든 입력 단위와 숨겨진(hidden) 단위에 적용하기 위해 다른 binary mask를 무작위로 샘플링한다. 1의 mask 값을 샘플링할 확률은 훈련을 시작하기 전에 고정된 하이퍼 파라미터이다. 일반적으로 입력 단위는 0.8의 확률을 사용하고 숨겨진 단위는 0.5의 확률을 사용한다.
Weight Scaling Inference Rule
그러나 훨씬 더 좋은 접근법은 단 하나의 forward 전파(propagation) cost로 전체 앙상블의 예측에 대한 좋은 근사치를 얻을 수 있게 해주는 것이다. 그렇게 하기 위해, 앙상블 멤버의 예측 분포의 산술 평균보다는 기하(geometric) 평균을 사용한다. Warde-Farley et al.(2014) 에서는 기하 평균이 산술 평균과 동등하게 수행된다는 주장과 경험적(empirical) 증거를 제시한다. 정규화되지 않은 확률 분포는 기하평균에 의해 다음과 같이 직접 정의된다. $$ \tilde{p}_{\text {ensemble }}(y | \boldsymbol{x})=\sqrt[2^{d}]{\prod_{\mu} p(y | \boldsymbol{x}, \boldsymbol{\mu})} $$ 여기서 $d$는 dropped 될 수 있는 단위의 수이다. 여기서는 표현을 단순히하기 위해 $\mu$에 대한 균등(uniform) 분포를 사용하지만 불균등(nonuniform) 분포 또한 가능하다. 예측을 하기 위해서는 앙상블을 다음과 같이 renormalize 해야한다. $$ p_{\text {ensemble }}(y | \boldsymbol{x})=\frac{\tilde{p}_{\text {ensemble }}(y | \boldsymbol{x})}{\sum_{y^{\prime}} \tilde{p}_{\text {ensemble }}\left(y^{\prime} | \boldsymbol{x}\right)} $$ $p(y|x)$를 하나의 모델에서 평가함으로써 $p_{\text{ensemble}}$의 근사치를 구할 수 있다. 그 모델은 모든 단위를 포함하지만 단위 $i$를 벗어나는 가중치에 단위 $i$를 포함하는 확률을 곱한 것이다. 이러한 접근법을 weight scaling inference rule 이라 부른다. 깊은 비선형 네트워크에서 이 근사 추론 규칙의 정확성에 대해 아직 이론적인 argument는 없지만 경험적으로 매우 잘 작동된다.
비선형의 hidden units가 없는 모델의 많은 클래스의 경우 weight scaling inference rule이 정확하다. 간단한 예제로, 벡터 $v$로 표현되는 n개의 입력 변수를 가지는 소프트맥스 회귀 분류기는 다음과 같다. $$ P(\mathrm{y}=y | \mathbf{v})=\operatorname{softmax}\left(\boldsymbol{W}^{\top} \mathbf{v}+\boldsymbol{b}\right)_{y} $$ 이항 벡터 $d$를 가지는 인풋의 요소별(element-wise) 곱셈에 의해 하위 모델의 family를 다음과 같이 인덱싱할 수 있다. $$ \begin{align} P(\mathrm{y}=y | \mathrm{v} ; d)=\operatorname{softmax}\left(W^{\top}(d \odot \mathrm{v})+b\right)_{y} \notag\\ P_{\text {ensemble }}(\mathrm{y}=y | \mathbf{v})=\frac{\tilde{P}_{\text {ensemble }}(\mathrm{y}=y | \mathbf{v})}{\sum_{y^{\prime}} \tilde{P}_{\text {ensemble }}\left(\mathrm{y}=y^{\prime} | \mathbf{v}\right)} \notag\\ \tilde{P}_{\text {ensemble }}(\mathrm{y}=y | \mathbf{v})= \sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} P(\mathrm{y}=y | \mathbf{v} ; \mathbf{d})} \notag \end{align} $$ $$ \begin{align} &=\sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \operatorname{softmax}\left(\boldsymbol{W}^{\top}(\boldsymbol{d} \odot \mathbf{v})+\boldsymbol{b}\right)_{y}} \notag\\ &=\sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \frac{\exp \left(\boldsymbol{W}_{y,:}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y}\right)}{\sum_{y^{\prime}} \exp \left(\boldsymbol{W}_{y^{\prime}, :}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y^{\prime}}\right)}} \notag\\ &=\frac{\sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \exp \left(\boldsymbol{W}_{y,:}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y}\right)}}{\sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \sum_{y^{\prime}} \exp \left(\boldsymbol{W}_{y^{\prime},:}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y^{\prime}}\right)}}\notag \\ \end{align} $$ $$ \begin{aligned} \tilde{P}_{\text {ensemble }}(\mathrm{y}=y |&\mathbf{v}) \propto \sqrt[2^{n}]{\prod_{d \in\{0,1\}^{n}} \exp \left(W_{y, i}^{\top}(d \odot \mathrm{v})+b_{y}\right)} \end{aligned} $$ $$ \begin{array}{c}=\exp \left(\frac{1}{2^{n}} \sum_{\boldsymbol{d} \in\{0,1\}^{n}} \boldsymbol{W}_{y,:}^{\top}(\boldsymbol{d} \odot \mathbf{v})+b_{y}\right) \\ =\exp \left(\frac{1}{2} \boldsymbol{W}_{y,:}^{\top} \mathbf{v}+b_{y}\right)\end{array} $$ weight scaling rule은 비선형성이 있는 deep 모델에 대한 근사치일 뿐이다. 비록 근사치가 이론적으로 특징되어지지 않지만, 경험적으로 잘 작동하는 경우가 많다.
Advantages of Dropout
Srivastava et al. (2014)에서는 weight decay, filter norm constraints, sparse activity regularization과 같은 계산적으로 inexpensive한 표준 정규화 방법보다 dropout이 더 효과적이라는 것을 보였다. 드랍아웃의 장점은 계산적으로 매우 cheap하다는 것이다. 트레이닝을 할 때 드랍아웃을 사용하는 것은 example 업데이트당 O(n)계산만 하면 된다. 또한 역전파(back propagation) 단계까지 이진수를 저장하기 위해 O(n) 메모리가 요구된다. 또 다른 중요한 장점은 사용할 수 있는 모델이나 트레이닝 절차의 타입을 제한하지 않는다는 것이다. 분포로 표현한 거의 모든 모델에서 잘 작동하고 stochastic gradient descent로 트레이닝 될 수 있다.
dropout의 상당 부분은 hidden units에 masking noise가 적용된다는 사실에서 발생한다는 점을 이해하는 것이 중요하다. 이것은 입력값의 raw values 보다 information content에 대한 고도의 지능적이고 적응적인 destruction 형태로 볼 수 있다. 원래 값보다 추출된 특징을 파괴하면 destruction 프로세스가 지금까지 획득한 입력 분포에 대한 모든 지식을 사용할 수 있다.