Fundamentals about Mathematical Optimization
Optimization Problem은 변수(variables), 제약식(constraints), 목적함수(objective function)로 구성되어있다. 모든 제약식을 만족하는 변수를 가질 때 feasibility를 유지하며 목적함수는 솔루션의 품질을 결정한다. 모든 feasible solution 중에서 가장 좋은 목적함수 값을 가질 때 최적(optimal)이라 한다. Primal bound는 지금까지 찾은 best solution의 목적함수 값이며 이를 incumbent solution이라고도 부른다. Dual bound 또한 best solution의 bound를 나타내며 지금까지 찾은 어떤 솔루션도 이 bound보다 좋지 않음을 나타낸다. Primal과 Dual bound를 통해 gap을 계산할 수 있고 gap이 0이 되는 순간 incumbent solution이 optimal임이 수학적으로 증명된다. 따라서 gap이 0이 아닌 경우 현재 솔루션(current solution)을 어떻게 개선할 것인지 고민해봐야한다.
목적지에서 도착지까지 가장 짧은 경로를 찾는 문제를 생각해보자. 우리가 흔히 구글맵에서 길을 찾을 때 나오는 경로는 optimal이 아닌 휴리스틱 솔루션이다. 정확한 optimal값보다는 적당히 좋은 feasible한 경로를 빠른 시간안에 찾기 위해 휴리스틱 솔루션을 채택한다. 이러한 휴리스틱 솔루션이 Primal bound(upper bound)가 되고 목적지에서 도착지까지의 직선거리(bee line)를 Dual bound(lower bound)로 생각할 수 있다. bound를 이용하여 gap을 구할 수 있으며 이를 통해 현재 솔루션의 품질을 알 수 있다.
Linear Programming(LP)은 선형식의 목적함수와 제약식을 가지며 모든 변수가 실수(real values)인 문제를 말한다. LP는 standard form으로 표현되며 이는 모든 선형 제약식이 등식(equation)으로 주어지고 모든 변수가 음수가 아닌(non-negative) 조건을 가진다는 것이다. 주어진 문제의 feasible solution 집합은 polyhedron으로 정의되며 이는 convex set이다. convex set을 가지는 convex function을 최적화하는 문제는 풀기 쉽다. 즉, polynomial time안에 문제를 풀 수 있다. standard form은 약간의 변형을 통해 다양한 form으로 나타낼 수 있다. 예를 들어 목적함수 벡터에 -1을 곱하여 minimize 문제를 maximize 문제로 바꾸거나 등식을 부등식(inequlity formulation) 형태로 바꿀 수 있고, slack variable을 추가하여 똑같은 식을 다양하게 표현할 수도 있다. Integer Program(IP)의 제약식은 주로 부등식으로 표현되고 LP와 비슷하지만 모든 변수가 정수(integer)이다. 이 때 정수조건이 없는 경우를 LP relaxation이라 한다. IP의 feasible solution 집합은 convex가 아닌 discrete set이고 이러한 nonconvexity 때문에 IP는 풀기 어렵다. Mixed Integer Program(MIP)은 LP와 IP가 합쳐진 문제라고 생각하면 된다. MIP에 사용되는 변수는 실수(real values)나 정수(integer)로 표현된다.
LP History
지금처럼 LP를 formulation하여 표현하는 방식은 옛날부터 있었던 것은 아니다. Gaussian elimination의 경우에도 Gauss가 이를 직접 표현하진 않았다. 1827년 Fourier는 variable elimination method를 사용했고 오늘날 Fourier-Motzkin elimination(Motzkin 1936)이라 불리며, 이를 하나의 변수와 부등식을 추가함으로써 LP solver로 바꿀 수 있다. 따라서 feasibility 문제를 풀어 최적화 문제를 풀 수 있게 된 것이다.
처음 LP를 formulation한 것은 1939년 George J. Stigler이고 그는 영양성분을 고려하여 가능한 가장 저렴한 식단을 구하는 문제를 풀었다. 이 당시에는 컴퓨터가 발명되기 전이기 때문에 그는 휴리스틱 방법으로 문제를 풀었고 0.7%의 optimality gap을 가지는 솔루션을 도출하였다. 그 후 LP는 빠르게 발전하여 1939년 Kantorovich는 현재까지 사용되는 LP 관련 용어를 만들어 LP의 기초를 다졌고, 1947년 Dantzig가 primal simplex algorithm을 만들었다. 이는 LP를 효율적으로 푸는 첫 번째 알고리즘이었고 최적화 분야에서 가장 중요한 혁신적인 사건이었다. 7년 후 1954년, Lemke와 Beale는 dual simplex algorithm을 소개했고 계속해서 다양한 심플렉스 변형들이 개발되었다.
1953년 발표된 'Computational Experience in Solving Linear Programs' 라는 논문에서는 처음으로 계산 실험이 이루어졌고 3가지 방법으로 LP를 풀었다. Feasibility tolerances나 memory limit 같이 현재까지도 다루어지는 부분을 언급하였다. 1954년 첫 상용 LP-Code가 등장했고 1960년대에 특히 석유회사에서 LP를 많이 사용하였다. 1972년에는 첫 상용 IP solver가 개발되었다.
Polyhedral theory
Polyhedra는 LP와 밀접한 관련이 있으며 다음 사이트에서 다양한 Polyhedra 모형을 볼 수 있다. LP는 $n$차원 벡터 공간에서 부등식의 집합에 대한 솔루션을 찾는 것이고 Polyhedron은 유한하게 많은 halfspace들의 교집합으로 정의된다. 각 선형 부등식이 halfspace로 정의되기 때문에 LP의 feasible solution 집합은 polyhedron으로 해석될 수 있다. Polytope은 유한하게 많은 점들의 convex hull로 정의되고 Convex polyhedral cone은 유한히 많은 점들의 conic combination(nonnegative linear combination)으로 정의된다. conic comination은 음수가 아닌(non-negative) 계수만을 사용하는 linear combination을 의미한다.
P라는 polyhedron을 생각해보자. P는 유한히 많은 halfspace들의 교집합이다. 즉, 행렬 A와 벡터 b가 존재한다($P = \{x \in \mathbb{R}^n | Ax \leq b\}$, outer representation). 또한, P는 convex polytope과 유한하게 생성된 polyheral cone의 합이다. 즉, 유한집합 V와 E가 존재한다($P = \text{conv}(V) + \text{conv}(E)$, inner representation).
$n$차원 polytope의 몇 가지 중요한 special case가 있다. 첫번째는 simplex로 0과 모든 unit vector의 convex hull이다. 이는 $n$+1의 vertice를 가지는 polytope이므로 $n$+1의 point를 가지는 convex hull로 표현될 수 있다. 또한, $n$+1의 facet을 가지므로 $n$+1의 부등식의 교집합으로 표현될 수 있다. 3차원 공간에서 심플렉스는 tetrahedron으로 알려져있다. 두번째는 cross polytope으로 plus identity vector와 minus identity vector의 convex hull이다. 이는 2$n$의 point를 가지는 convex hull로 표현될 수 있고 $2^n$의 부등식의 교집합으로 표현될 수 있다. 마지막으로 cube는 $n$차원 공간에서 모든 가능한 plus 1, minus 1 조합의 convex hull이다. 이는 $2^n$의 extreme point를 가지며 부등식을 통해 큐브를 표현하기 위해서는 차원당 2$n$개의 부등식이 필요하다.
Farkas Lemma는 수리 최적화에서 매우 중요한 이론 중 하나이다. 이는 부등식의 valid combination을 적용하여 false statement를 도출함으로써 infeasible LP에 대해 알려준다. Farkas Lemma는 $Ax \leq b$ 또는 $yA = 0, yb < 0 $ 중 하나만이 솔루션을 갖도록 formulation될 수 있고 Theorems of Alternatives로 불리는 Theorem class에 속한다. 또한 Duality theorems, Complementary slackness, Proof of LP optimality 등의 중요한 higher-level LP 이론의 기초가 된다.
Farkas Lemma를 증명하는 한 가지 방법은 Fourier-Motzkin Elimination(FME)을 사용하는 것이다. 이는 변수 하나를 제거하여 $n$차원 공간을 $n$-1차원 공간으로 줄이는 방법이다. 이때 polyhedron이 nonempty인지 확인해야 한다. 각 elimination step은 worst case에서 총 $O(m^{2^n})$의 running time이 소요될 수 있으므로 실질적으로 다루기 어렵다. FME는 보통 polyhedral transformation 방법으로 잘 알려져 있고 trick을 사용하여 cube나 cross polytope을 single exponential running time으로 줄일 수는 있다. FME를 통해 polyhedral 이론과 LP 이론을 연결할 수 있다.
LP theory
다음과 같은 LP 문제를 가정해보자. $$ \begin{aligned} \min\{c^Tx| Ax \geq b, x \geq 0\} \end{aligned} $$
이 문제에 대한 어떤 feasible한 솔루션을 알고있다고 가정했을 때, 솔루션의 품질을 어떻게 증명할 수 있을까? 이를 Farkas Lemma와 비슷한 trick을 사용하여 증명할 수 있다. 제약식 양변에 양수값을 곱해도 똑같다는 특징과 두 개의 valid constraints를 더한 제약식은 여전히 valid constraint라는 특징을 이용한다. 목적함수의 maximal underestimator인 모든 제약식의 conic combination을 찾고 이를 LP로 표현한 것을 dual LP라 부른다. 위 식의 dual LP는 다음과 같이 표현할 수 있다.
$$ \begin{aligned} \max\{y^Tb| y^TA \leq c, y \geq 0\} \end{aligned} $$
primal LP에서 각 제약식은 dual LP에서 변수가 되고, primal LP에서 각 변수는 dual LP에서 제약식이 된다. 목적함수는 primal에서 minimize면 dual에서는 maximize가 되며, $\geq$ 제약식은 $\leq$ bound, $\leq$ 제약식은 $\geq$ bound, = 제약식은 free variable이 된다.
이제 듀얼의 특성에 대해 알아보자.
$$ \begin{aligned} \max\{y^Tb| y^TA \leq c, y \geq 0\} \leq \min\{c^Tx| Ax \geq b, x \geq 0\} \end{aligned} $$
dual LP의 솔루션과 Primal LP의 솔루션이 위와 같은 관계를 가진다는 것이 Weak Duality Theorem이다. 위 식은 $y^Tb \leq y^T(Ax) = (y^TA)x \leq c^Tx$를 통해 증명할 수 있다. (Trivial to proof)
$$ \begin{aligned} \max\{y^Tb| y^TA \leq c, y \geq 0\} = \min\{c^Tx| Ax \geq b, x \geq 0\} \end{aligned} $$
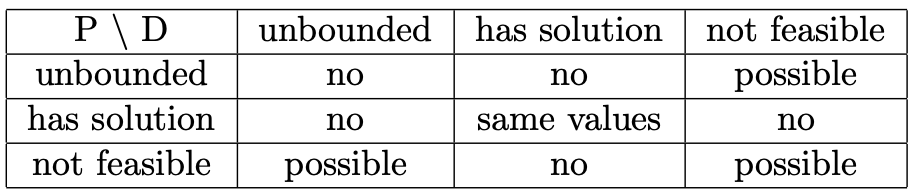
Strong Duality Theorem은 최적화 분야에서 가장 중요한 이론이라 할 수 있다. dual이 finite optimum을 가지는 경우에만 primal이 finite optimum을 갖고 위의 식처럼 두 값이 같다는 이론이다. 즉, 최적해가 결정되면 두 문제의 목적함수 값은 같아진다는 것이다. 이를 증명하는 것은 어렵지만 weak duality와 Farkars lemma를 사용하여 증명할 수는 있다. Primal과 dual 모두 unbounded, has solution, not feasible(infeasible)일 수 있는데 각각에 대해 다음과 같은 관계를 가진다.
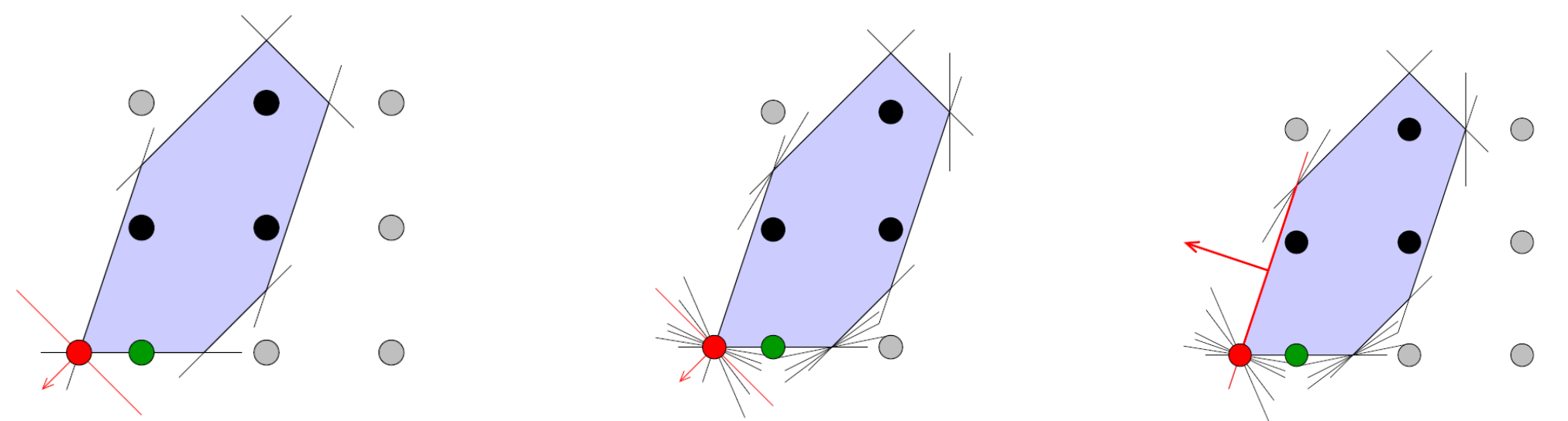
Complementary Slackness는 primal과 dual의 관계를 나타내고 솔루션이 최적인지 아닌지 확인할 수 있는 방법이다(CS Condition). 이는 binging 여부와 관계가 있으며 (P)가 솔루션 $x^*$를 가지고 (D)가 솔루션 $y^*$를 가진다고 가정했을 때 다음과 같은 관계를 가진다.
$$ \begin{aligned} & \textit{1. If $x^∗_j$ > 0, then the $j$th constraint in (D) is binding.} \\ & \textit{2. If the $j$th constraint in (D) is not binding, then $x^∗_j$ = 0.} \\ & \textit{3. If $y^*_i$ > 0, then the $i$th constraint in (P) is binding.} \\ & \textit{4. If the $i$th constraint in (P) is not binding, then $y^*_i$ = 0.} \end{aligned} $$
이는 어떤 문제의 변수와 그와 연관된 제약식의 관계((primal variable, dual constraint) or (primal constraint, dual variable))를 나타내며 동시에 slack을 가질 수 없다는 것이다. dual variable이 0일 때, primal constraint가 binding인 것은 가능하지만 (즉, no slack in two places) dual variable이 양수일 때, primal constraint가 slack(non-binding)을 갖는 것은 불가능하다. 이러한 특성 때문에 상보여유(complementary slackness)라 부르는 것이고, 이 이론은 dual 문제와 변수에 대한 해석에 도움을 주기 때문에 매우 유용하다. dual variable은 shadow price로도 해석될 수 있는데 이는 특정한 제약식이 relaxed 된다면 목적함수 값이 얼만큼 변하는지를 나타낸다.
강의 영상 : LP & Polyhedral Theory