Simplex Algorithm
심플렉스 알고리즘은 기하학적 직관(geometry intuition)으로 다음과 같이 나타낼 수 있다.
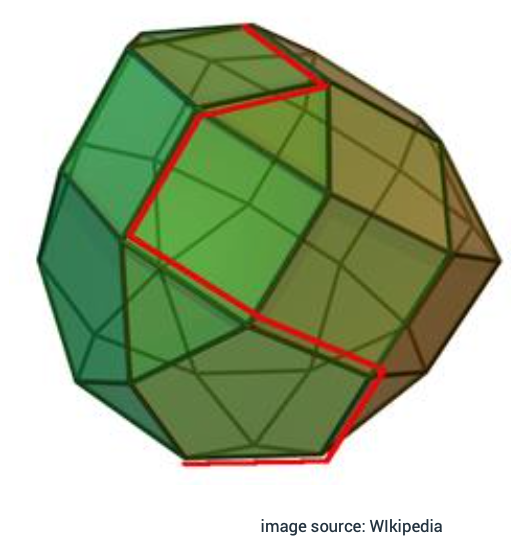
그림에서 보이듯 알고리즘은 어떤 꼭짓점(vertex)에서 꼭짓점으로 이동한다. 두 꼭짓점 사이의 변(edge)을 따라서 움직이며 현재 위치에서 목적 함수값을 좋게 하는 근처 꼭짓점으로 이동한다. 이러한 프로세스를 pivoting이라 하고 만약 더 이상 목적 함수값을 개선하는 꼭짓점이 없다면 알고리즘은 종료된다. 즉, 현재 위치가 optimal solution이 되는 것이다. 이 때 만약 목적함수가 ray를 따라 움직인다면 이는 LP가 unbounded가 되는 것을 증명한다.
심플렉스 알고리즘의 특징은 다음과 같이 정리할 수 있다.
- 목적함수가 polyhedron의 경계(boundary)에서 최적이 된다. (convexity)
- 최적해는 항상 꼭짓점에 존재하며 이 때 목적함수와 모든 제약식은 선형이어야 한다. (linearity)
- local optimality가 global optimality와 동일하다. (convexity)
위 식에서 행렬 $A$와 $x$를 다음과 같이 표현해보자.
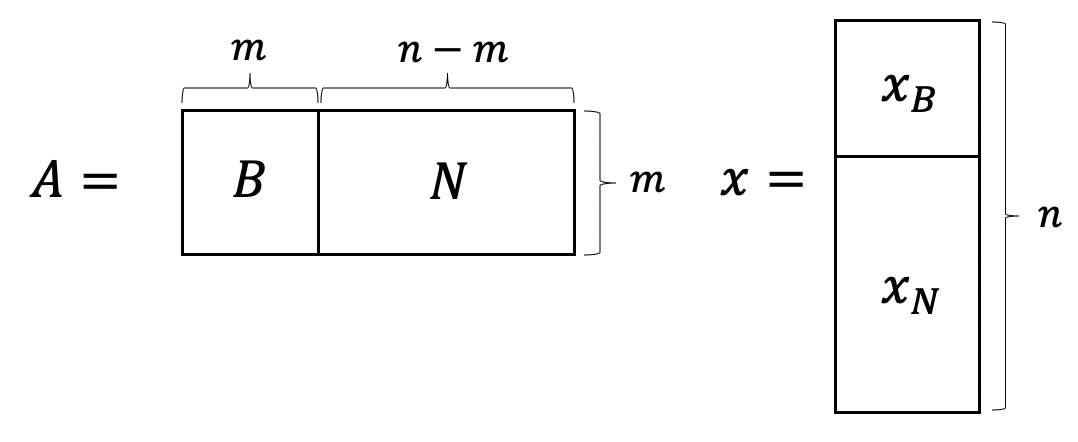
심플렉스 알고리즘의 아이디어는 LP가 optimal solution을 갖는다면 꼭짓점 중 하나에서 항상 optimal soltuion을 갖는 것에서 시작했다. 각 꼭짓점에 대해 basic solution이 있고 항상 optimal basic solution이 있다. 이는 이론적으로 행렬의 모든 가능한 bases를 제거함으로써 LP를 풀 수 있다는 의미이다. (제거해야하는 가능한 솔루션 후보의 수는 유한하게 있다.) 따라서 심플렉스 알고리즘의 아이디어는 feasible start basis를 찾은 후 feasibility를 유지하면서 목적함수값을 좋게 만다는 basis에 있는 column 중 하나와 non-basis에 있는 column을 바꾸면서 optimal solution을 찾을 때까지 반복하는 것이다. (즉, 수많은 방향 중 basic diretion으로 계속 이동하며 optimal을 찾는 것이다.)
그렇다면 pivoting할 column은 어떻게 고르는 것일까? 이는 reduced cost 계산을 통해 고르게 되는데 reduced cost를 계산하면 어떤 방향으로 갔을 때 얼만큼 목적함수 값을 좋게 하는지 알 수 있다. 만약 모든 reduced cost 값이 non-negative인 경우 현재 솔루션이 optimal이 된다. 심플렉스 알고리즘 방법을 예시를 통해 알아보자.
Example - Unbounded Solution $$ \begin{aligned} \max \quad & -x_1 - 3x_2 \\ s.t. \quad & 2x_1 + 5x_2 \leq 12 \\ & x_1 + x_2 \geq 1 \\ & x_1 \geq 0 \end{aligned} $$ 우선 주어진 문제를 심플렉스 방법으로 풀기 위해서는 먼저 Standard Form으로 바꿔야한다. Standard Form은 (1) 모든 변수가 non-negativity이고 (2) 제약식은 equality 제약을 가지며 (3) 제약식의 우변이 양수값을 가져야한다. 따라서 다음과 같이 바꿀 수 있다. $$ \begin{aligned} \max \quad & -x_1 - 3x_2 \\ s.t. \quad & 2x_1 + 5x_2 + x_3 = 12 \\ & x_1 + x_2 - x_4 = 1 \\ & x_1 \geq 0, x_3 \geq 0, x_4 \geq 0 \end{aligned} $$ 이 때 $\leq$ 을 $=$로 바꾸기 위해 사용된 변수 $x_3$를 slack variable, $\geq$ 을 $=$로 바꾸기 위해 사용된 변수 $x_4$를 surplus variable이라 한다. 새로 추가된 변수는 (1)을 만족해야하므로 non-negativity 제약을 추가해준다. 그렇다면 이제 Standard Form으로 모두 바꾼걸까? 언뜻 보기에는 Standard Form처럼 보이지만 $x_2$가 non-negativity라는 조건이 주어지지 않았다. 이는 $x_2$가 어떤 값도 가능한 free variable이라는 것을 뜻한다. 따라서 $x_2 = x_5 - x_6$으로 나타내보자. $$ \begin{aligned} \max \quad & -x_1 - 3x_5 + 3x_6 \\ s.t. \quad & 2x_1 + 5x_5 - 5x_6 + x_3 = 12 \\ & x_1 + x_5 - x_6 - x_4 = 1 \\ & x_1 \geq 0, x_3 \geq 0, x_4 \geq 0, x_5 \geq 0, x_6 \geq 0 \end{aligned} $$ 이제 Standard Form의 조건을 모두 만족하므로 심플렉스 방법으로 문제를 풀어보자. 우선 목적함수는 $z = -x_1 - 3x_5 + 3x_6$라 하자. (이 때 $z$는 decision variable은 아니다.) 따라서 다음과 같이 나타낼 수 있다.




그렇다면 이번에는 좀 더 간단한 예시를 통해 optimal solution을 가지는 문제를 풀어보자. $$ \begin{aligned} \max \quad & -3x_1 + 2x_2 \\ s.t. \quad & -3x_1 + 3x_2 + x_3 = 6 \\ & -4x_1 + 2x_2 + x_4 = 2 \\ & x_1 \geq 0, x_2 \geq 0, x_3 \geq 0, x_4 \geq 0 \end{aligned} $$ 앞서 본 예제와 똑같은 방법으로 위 문제를 simplex tableaus로 나타내면 다음과 같다. $x_2$의 계수가 양수이기 때문에 entering variable로 설정한다. $x_3 = 0$ 또는 $x_4 = 0$이 되기 위해서는 $\Delta$ 가 2 또는 1이 되어야한다. $\Delta$가 2가 되면 1보다 목적함수 값을 더 좋게 하지만 $x_4$가 음수값이 되어버린다. 따라서 feasibility를 유지하면서 목적함수 값을 가장 좋게 만드는 $\Delta$ 는 1이다. 그러므로 $x_4$를 leaving variable로 설정한다. 이 때 minimum ratio rule을 통해 간단하게 계산할 수도 있다. 제약식의 우변 값을 entering variable의 column값(양수인 값만 비교)으로 나눴을 때 제일 작은 값을 선택하는 것이다. 즉, min(6/3,2/2) = 1 이다.



이번에는 alternative optimal solution, 즉, 하나 이상의 optimal solution을 갖는 경우에 대해 알아보자. $$ \begin{aligned} \max \quad & 2x_1 + 4x_2 \\ s.t. \quad & x_1 + x_2 + x_3 = 3 \\ & 0.5x_1 + x_2 + x_4 = 2.5 \\ & x_1 \geq 0, x_2 \geq 0, x_3 \geq 0, x_4 \geq 0 \end{aligned} $$ 계수가 가장 큰 $x_2$를 entering variable, minimum ratio rule에 의해 $x_4$를 leaving variable로 설정한다.

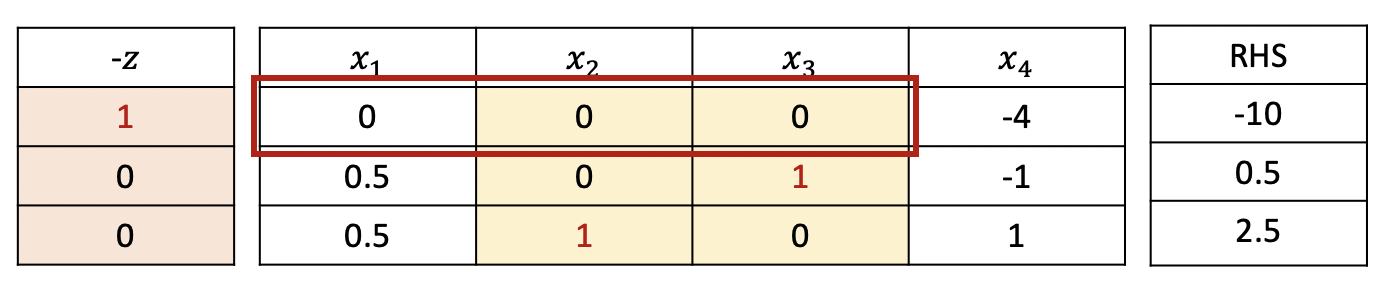
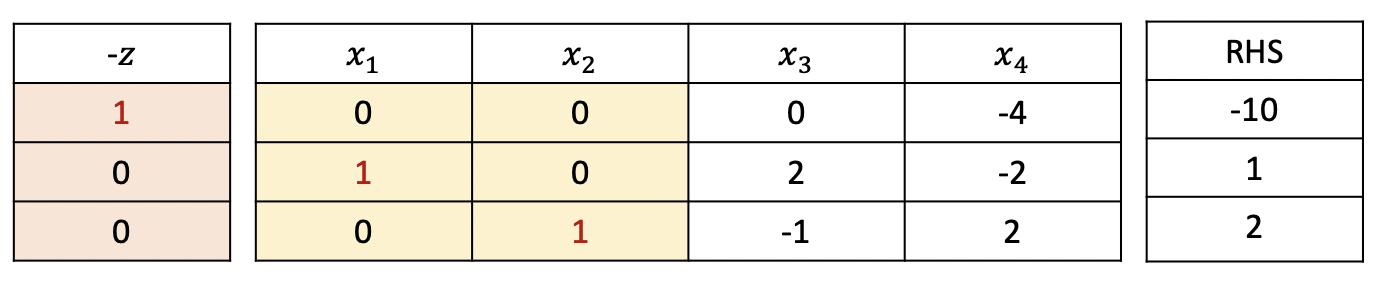
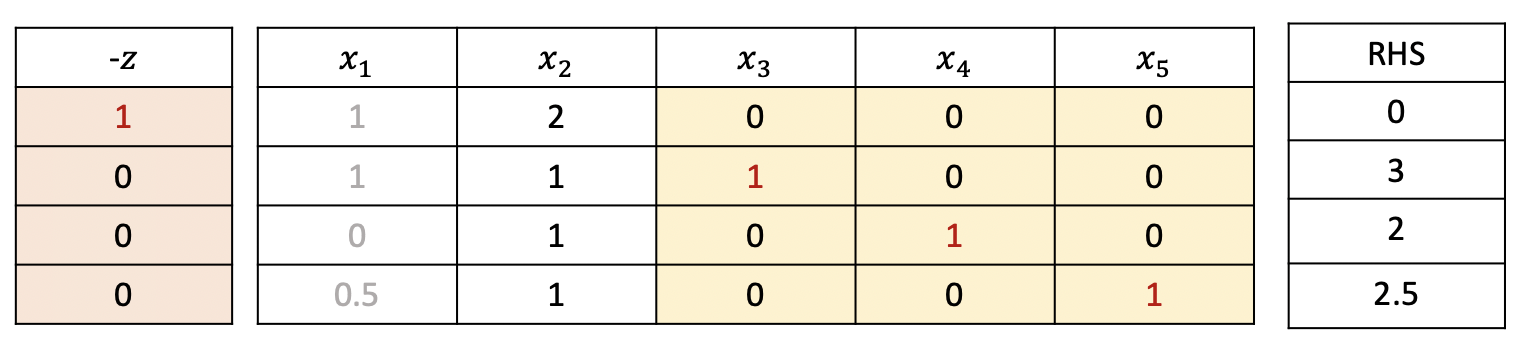
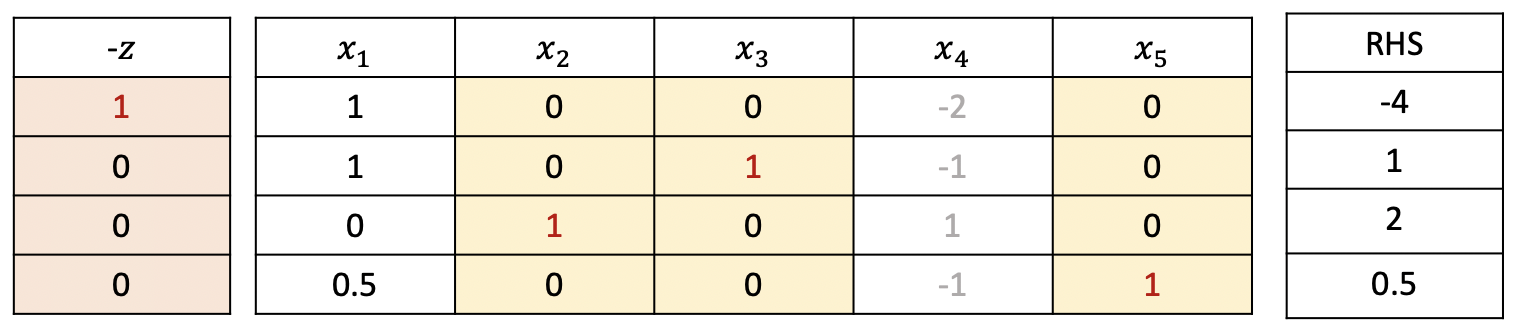
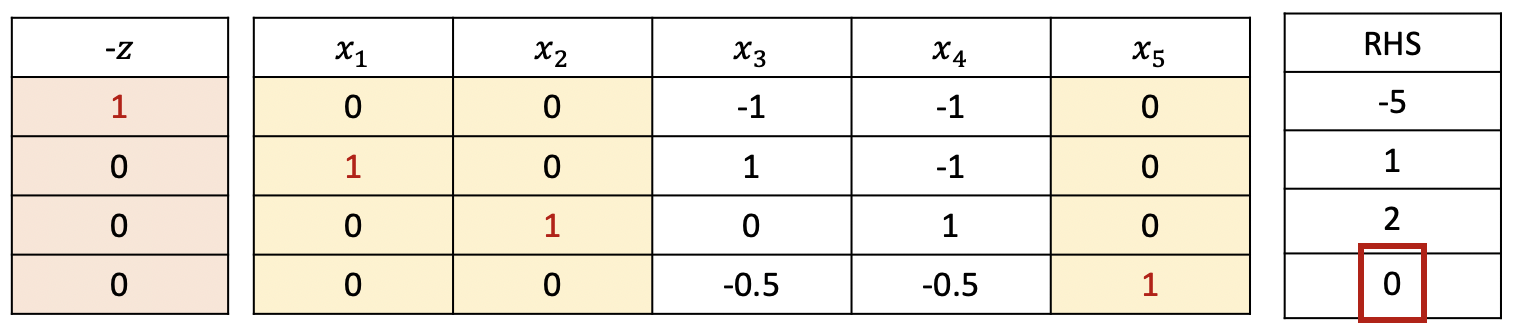
이번에는 degeneracy가 발생하는 경우에 대해 알아보자. $$ \begin{aligned} \max \quad & x_1 + 2x_2 \\ s.t. \quad & x_1 + x_2 + x_3 = 3 \\ & x_2 + x_4 = 2 \\ & 0.5x_1 + x_2 + x_5 = 2.5 \\ & x_1 \geq 0, x_2 \geq 0, x_3 \geq 0, x_4 \geq 0, x_5 \geq 0 \end{aligned} $$ 계수가 가장 큰 $x_2$를 entering variable, minimum ratio rule에 의해 $x_4$를 leaving variable로 설정한다.
강의 영상 : Theory and Basics