Lagrangian Relaxation
다음과 같은 IP(Integer program)를 생각해보자. $$ \begin{aligned} \text{(IP)} \quad &z=\max cx \\ &Ax \le b \\ &Dx \le d \\ &x \in Z^n_+ \end{aligned} $$ 어떤 제약조건만 있는 IP는 쉽게 풀린다는 관점에서 $Ax \le b$ 식을 "nice"하다고 가정해보자. 그러면 복잡한(complicating) 제약식 $Dx \le d$만 없다면 원래 IP 문제를 푸는 것 보다 relaxation이 더 쉬워진다. 많은 문제들이 이처럼 나이스한 제약과 복잡한 제약을 동시에 갖고 있는데, 복잡한 제약을 없앨 수 있다면 쉽게 문제를 풀 수도 있을 것이다. 예를 들어 TSP (traveling salesman problem)의 connectivity 제약식, UFL(uncapacitated facility location)의 client demand 제약식 등 복잡한 제약을 없앨 수 있다면 말이다. 그러나 그냥 없애버리면 중요한 제약식이 전부 무시되기 때문에 relaxation의 bound가 매우 좋지 않으므로 Lagrangian relaxation을 사용하고자 한다.
IP 문제를 좀더 간단하게 일반적인 폼 (general form)으로 바꿔보자. $$ \begin{aligned} &z=\max cx \\ &Dx \le d \\ &x \in X \end{aligned} $$ 여기서 $Dx \le d $는 $m$개의 복잡한 제약식이다.
어떤 값 $u = (u_1, ... , u_m) \ge 0$ 에 대해 다음과 같이 IP의 relaxation을 정의하자. $$ \begin{aligned} \text{(IP(u))} \quad &z(u)=\max cx + u(d-Dx)\\ &x \in X \end{aligned} $$ IP($u$)는 $\{x : Dx \le d, x \in X\} \subseteq X $ 이므로 feasibel region은 같거나 크고, $u \ge 0$ 이고 모든 $x \in X$에 대해 $(d-Dx) \ge 0$이므로 목적값(objective value) 또한 원래 IP 문제보다 같거나 크다.
IP($u$)에서 복잡한 제약식이 목적함수의 penalty term인 $u(d-Dx)$으로 추가됨으로써 다루어지는 것을 볼 수 있다. 이 때 $u$ 를 $Dx \le d$ 제약에 대한 Lagrange multiplier (price, dual variable) 라고 한다.
따라서 IP($u$)를 파라미터 $u$를 가진 IP의 Lagrangian relaxation (subproblem)이라 부른다. IP($u$)는 IP의 relaxation이기 때문에 $z(u) \ge z$이고 IP의 최적값(opmial value)의 upper bound를 얻을 수 있다. 가장 좋은 upper bound를 찾기 위해 Lagrangian Dual Problem을 푼다.
1에 의해 $w_{LD} \le z(u)$이고, 3에 의해 $cx(u)+u(d-Dx(u)) = cx(u)$이다. 2에 의해 $x(u)$는 IP에서 feasible이고 따라서 $cx(u) \le z$ 이다. 그러므로 $w_{LD} \le z(u) = cx(u) \le z$이고 equality 제약으로 인해 $w_{LD} \ge z$이므로 $x(u)$는 IP에서 optimal이다.
Application - UFL
UFL 문제에 이를 적용해 보자. 먼저, strong formulation으로 시작한다. $$ \begin{aligned} \text{(IP)} \quad z=\max &\sum_{i \in M} \sum_{j \in N} c_{ij}x_{ij} - \sum_{j \in N} f_j y_j \\ &\sum_{j \in N} x_{ij} = 1 \quad \forall i \in M \\ &x_{ij}-y_j \le 0 \quad \forall i \in M, j \in N \\ &x \in R^{|M|\times|N|}, y \in B^{|N|} \end{aligned} $$ demand 제약식을 dualizing한다. $$ \begin{aligned} \text{(IP($u$))} \quad z=\max &\sum_{i \in M} \sum_{j \in N} (c_{ij}-u_i)x_{ij} - \sum_{j \in N} f_j y_j + \sum_{i \in M}u_i \\ &x_{ij}-y_j \le 0 \quad \forall i \in M, j \in N \\ &x \in R^{|M|\times|N|}, y \in B^{|N|} \end{aligned} $$ 이는 각 location에 대한 subproblem으로 갈라진다. $$ \begin{aligned} \text{(IP}_j(u)) \quad z_j(u)=\max &\sum_{i \in M} (c_{ij}-u_i)x_{ij} - f_j y_j \\ &x_{ij}-y_j \le 0 \quad \forall i \in M \\ &x_{ij} \ge 0 \quad \forall i \in M, y_i \in B^1 \end{aligned} $$ 따라서 $IP_j(u)$이면 $z(u) = \sum_{j \in N} z_j(u) + \sum_{i \in M} u_i$이다. 만약 $y_j = 0$이면 모든 $i$에 대해 $x_{ij} = 0$이고 목적값은 0이 된다. 만약 $y_j=1$이면 profitable한 모든 고객은 서비스를 받으므로 $c_{ij}-u_i >0$이다. 따라서 $z_j(u) = \max \{0, \sum_{i \in M} \max [c_{ij}-u_i, 0]-f_j\}$이다.
UFL Example
이와 관련된 간단한 예시를 들어보자. $m = 6$인 clients와 $n=5$인 potential locations가 있고 fixed location cost $f = (2,4,5,3,3)$이고 client-location profit matrix($c_{ij}$)는 왼쪽과 같다고 하자. $u=(5,6,3,2,5,4)$라 하면 ($c_{ij}-u_i$)를 오른쪽과 같이 나타낼 수 있다.
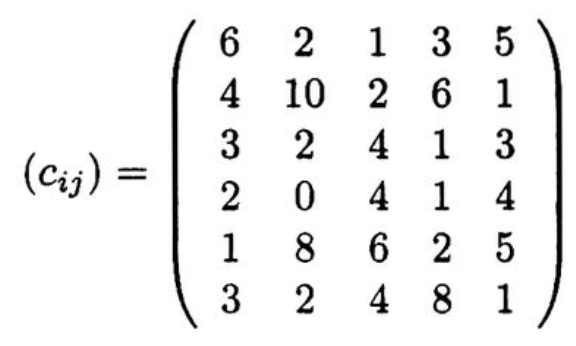
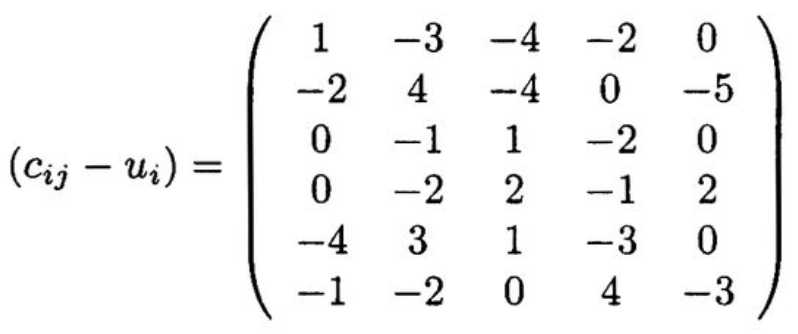
모든 $j = 2$에 대해 $y_2=0$이면 0의 값을 얻고 $y_2=1$이면 $x_{22}=1$, $x_{52}=1$로 설정하여 $y_2=1$인 net profit이 7-4 = 3이 된다. 그러므로 $z_2(u)=3$을 주는 $y_2=1$로 설정하는 것이 optimal 이다. 각 depot에 대해 비슷한 계산을 수행하면 IP($u$)의 optimal solution은 $y_1=y_3=y_5=0$, $y_2=x_{22}=x_{52}=1$, $y_4 = x_{64}=1$로 세팅하면 $z(u) = 3+1+\sum_{i \in M} u_i = 29$ 이다.
다음과 같은 IP(Integer program)를 생각해보자. $$ \begin{aligned} \text{(IP)} \quad &z=\max cx \\ &Ax \le b \\ &Dx \le d \\ &x \in Z^n_+ \end{aligned} $$ 어떤 제약조건만 있는 IP는 쉽게 풀린다는 관점에서 $Ax \le b$ 식을 "nice"하다고 가정해보자. 그러면 복잡한(complicating) 제약식 $Dx \le d$만 없다면 원래 IP 문제를 푸는 것 보다 relaxation이 더 쉬워진다. 많은 문제들이 이처럼 나이스한 제약과 복잡한 제약을 동시에 갖고 있는데, 복잡한 제약을 없앨 수 있다면 쉽게 문제를 풀 수도 있을 것이다. 예를 들어 TSP (traveling salesman problem)의 connectivity 제약식, UFL(uncapacitated facility location)의 client demand 제약식 등 복잡한 제약을 없앨 수 있다면 말이다. 그러나 그냥 없애버리면 중요한 제약식이 전부 무시되기 때문에 relaxation의 bound가 매우 좋지 않으므로 Lagrangian relaxation을 사용하고자 한다.
IP 문제를 좀더 간단하게 일반적인 폼 (general form)으로 바꿔보자. $$ \begin{aligned} &z=\max cx \\ &Dx \le d \\ &x \in X \end{aligned} $$ 여기서 $Dx \le d $는 $m$개의 복잡한 제약식이다.
어떤 값 $u = (u_1, ... , u_m) \ge 0$ 에 대해 다음과 같이 IP의 relaxation을 정의하자. $$ \begin{aligned} \text{(IP(u))} \quad &z(u)=\max cx + u(d-Dx)\\ &x \in X \end{aligned} $$ IP($u$)는 $\{x : Dx \le d, x \in X\} \subseteq X $ 이므로 feasibel region은 같거나 크고, $u \ge 0$ 이고 모든 $x \in X$에 대해 $(d-Dx) \ge 0$이므로 목적값(objective value) 또한 원래 IP 문제보다 같거나 크다.
IP($u$)에서 복잡한 제약식이 목적함수의 penalty term인 $u(d-Dx)$으로 추가됨으로써 다루어지는 것을 볼 수 있다. 이 때 $u$ 를 $Dx \le d$ 제약에 대한 Lagrange multiplier (price, dual variable) 라고 한다.
따라서 IP($u$)를 파라미터 $u$를 가진 IP의 Lagrangian relaxation (subproblem)이라 부른다. IP($u$)는 IP의 relaxation이기 때문에 $z(u) \ge z$이고 IP의 최적값(opmial value)의 upper bound를 얻을 수 있다. 가장 좋은 upper bound를 찾기 위해 Lagrangian Dual Problem을 푼다.
IF $u \ge 0$,
1. $x(u)$는 IP($u$)의 optimal solution이고
2. $D(x) \le d$ 이고
3. $u_i > 0$일 경우, $(Dx(u))_i = d_i$
THEN $x(u)$는 IP의 optimal이다.
1. $x(u)$는 IP($u$)의 optimal solution이고
2. $D(x) \le d$ 이고
3. $u_i > 0$일 경우, $(Dx(u))_i = d_i$
THEN $x(u)$는 IP의 optimal이다.
1에 의해 $w_{LD} \le z(u)$이고, 3에 의해 $cx(u)+u(d-Dx(u)) = cx(u)$이다. 2에 의해 $x(u)$는 IP에서 feasible이고 따라서 $cx(u) \le z$ 이다. 그러므로 $w_{LD} \le z(u) = cx(u) \le z$이고 equality 제약으로 인해 $w_{LD} \ge z$이므로 $x(u)$는 IP에서 optimal이다.
Application - UFL
UFL 문제에 이를 적용해 보자. 먼저, strong formulation으로 시작한다. $$ \begin{aligned} \text{(IP)} \quad z=\max &\sum_{i \in M} \sum_{j \in N} c_{ij}x_{ij} - \sum_{j \in N} f_j y_j \\ &\sum_{j \in N} x_{ij} = 1 \quad \forall i \in M \\ &x_{ij}-y_j \le 0 \quad \forall i \in M, j \in N \\ &x \in R^{|M|\times|N|}, y \in B^{|N|} \end{aligned} $$ demand 제약식을 dualizing한다. $$ \begin{aligned} \text{(IP($u$))} \quad z=\max &\sum_{i \in M} \sum_{j \in N} (c_{ij}-u_i)x_{ij} - \sum_{j \in N} f_j y_j + \sum_{i \in M}u_i \\ &x_{ij}-y_j \le 0 \quad \forall i \in M, j \in N \\ &x \in R^{|M|\times|N|}, y \in B^{|N|} \end{aligned} $$ 이는 각 location에 대한 subproblem으로 갈라진다. $$ \begin{aligned} \text{(IP}_j(u)) \quad z_j(u)=\max &\sum_{i \in M} (c_{ij}-u_i)x_{ij} - f_j y_j \\ &x_{ij}-y_j \le 0 \quad \forall i \in M \\ &x_{ij} \ge 0 \quad \forall i \in M, y_i \in B^1 \end{aligned} $$ 따라서 $IP_j(u)$이면 $z(u) = \sum_{j \in N} z_j(u) + \sum_{i \in M} u_i$이다. 만약 $y_j = 0$이면 모든 $i$에 대해 $x_{ij} = 0$이고 목적값은 0이 된다. 만약 $y_j=1$이면 profitable한 모든 고객은 서비스를 받으므로 $c_{ij}-u_i >0$이다. 따라서 $z_j(u) = \max \{0, \sum_{i \in M} \max [c_{ij}-u_i, 0]-f_j\}$이다.
UFL Example
이와 관련된 간단한 예시를 들어보자. $m = 6$인 clients와 $n=5$인 potential locations가 있고 fixed location cost $f = (2,4,5,3,3)$이고 client-location profit matrix($c_{ij}$)는 왼쪽과 같다고 하자. $u=(5,6,3,2,5,4)$라 하면 ($c_{ij}-u_i$)를 오른쪽과 같이 나타낼 수 있다.
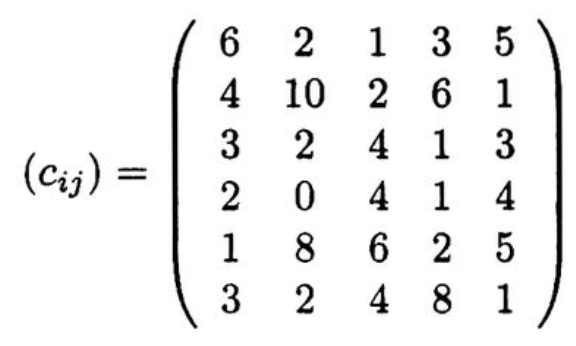
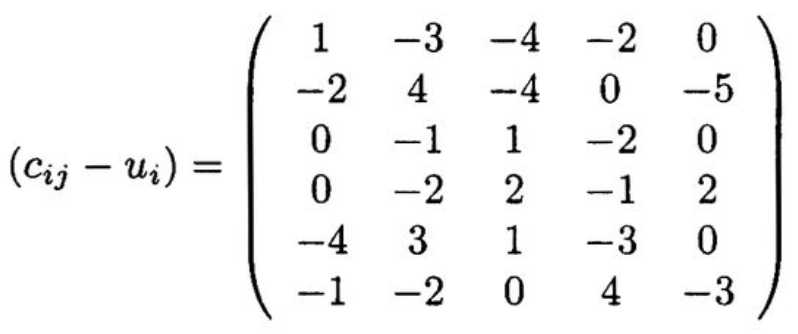
모든 $j = 2$에 대해 $y_2=0$이면 0의 값을 얻고 $y_2=1$이면 $x_{22}=1$, $x_{52}=1$로 설정하여 $y_2=1$인 net profit이 7-4 = 3이 된다. 그러므로 $z_2(u)=3$을 주는 $y_2=1$로 설정하는 것이 optimal 이다. 각 depot에 대해 비슷한 계산을 수행하면 IP($u$)의 optimal solution은 $y_1=y_3=y_5=0$, $y_2=x_{22}=x_{52}=1$, $y_4 = x_{64}=1$로 세팅하면 $z(u) = 3+1+\sum_{i \in M} u_i = 29$ 이다.